Evanh, it's in the /samples/fileserver/ directory. Just copy the spin file into this directory. I just modified an example from this directory for the file server.
Pic18f2550:
Ja, du musst sogar mit 500 kHz abtasten, da sonst das Sinc3 Filter überläuft. Deshalb hab ich in meinem Beispiel so eine tiefe clkfreq gewählt, um überhaupt auf 48 kHz runter zu kommen.
Ich würde 196.608MHz / 512 = 384 kHz wählen, das ist eine Standardfrequenz und der P2 wird nicht so stark übertaktet.
@evanh said:
The good news is if that spectrum is right then frequencies above ~20 Hz are 15+ ENOB.
If you choose other window types and a shorter FFT size, you see some bars at higher frequencies. That's why I don't really trust this frequency analysis results.
If somebody claims 18 or 24 bits of resolution or even accuracy I wouldn't believe him. Somewhere above 16 bits or 100dB SNR things become really complicated and expensive. I worked for a company that develops test equipment for automotive electronics around 2000. One project was to make an A/D converter which offers true 18 bit accuracy from DC to 100kS/s. 18 bits and a +/-10V input means ~80µV resolution and sounds not too hard. But the only way to implement this was to use the best stereo ADC we could get and use one channel for self-calibration and the other for the actual measurement. The ADC, the voltage reference, the multiplexer and all voltage dividers and amplifiers were put in a sealed, heated box regulated to 50°C+/-0.1. For the voltage dividers we had to use several ultra-precision resistors (0.1%, 10ppm/K) in series because a single resistor would drift too much because of self-heating from the current flow. We had to use special protection diodes because the leakage of standard zener or transzorb diodes would cause too much voltage drop in the input lines. And we found out that a $20,000 voltage reference from HP had too much noise. At the end we used normal but temperature controlled alcali batteries calibrated with a precision multimeter. But they had to be brand-new. If you draw 1mA for one second from them they need hours to stabilize, again. And if you play the "sound" of their voltage with extreme amplification it sounds like you hold your ear close to soda water. You can hear the chemistry in the cell working!
24 bits of resolution (~1µV @ 10V range) is possible with heavy low-pass filtering, for example, to monitor strain gauges or thermocouples. But if you need higher bandwidth than a few samples per second it gets really hard.
I downloaded all of Flexprop sources and found it in there. Then fixed another bug in fs9p.cc where it was oddly also not providing a length parameter to strncmp(). Compiled and it works.
Right what I changed is the sample data gain. Since it was just recording silence, it wouldn't clip when when above unity. So I went for x16 gain (20 bits effective) and removed the high four bits so it is still stored as 16-bit samples.
This has the effect of raising the noise floor by 24 dB when analysed:
That -72 dB at 20 kHz gets 48 dB subtracted to make it -120 dB (ENOB = 19.6). Best case of course.
And the -36 dB hump (minus 48) is a good match for the -84 dB in the original. Which is still ENOB = 13.6, which is better than I was expecting. I guess that's still not DC though.
Is this not too good to be true?
What have you connected at the ADC inputs?
Good trick to use only a 16 bit range of a 20 or 24 bit signal, and then add the reduced bits in dB later. I get similar results when I try that -> about 108 dB with 20 bits.
These graphs don't represent anything "absolute": the noise level at the particular frequency depends on FFT length. The more FFT samples, the more subbands, the less energy in one subband and the graph goes lower, while sum of all these subbands energy remains the same.
I got this "silent.wav" signal, converted it to 32 bit using (very old version of) Adobe Audition, and filtered out low and high frequencies. leaving 100..7000 Hz band, to make observation easier. Then I zoomed the waveform. There is 5-bit depth noise in this (sample values from about -16 to 16) and the noise (as sum of all subbands energy) in this band is at about -65 dB level (measured using Audition's level monitoring).
This is consistent with my earlier experiments.
When looking at the spectrum of original, unfiltered "silent.wav" using Audition's scanning and averaging at 65536 FFT samples, the 1/f nature of this noise is easy visible.
While the resulting real resolution is in this case 11 bits, the quality is not like 11-bit digital sampling (which is awful) but rather 16-bit ADC with noise added. The 1/f noise character is somewhat similar to the noise introduced by RIAA vinyl record preamps and 60-something dB SNR is also similar to good analog audio tape or good quality vinyl record. That's why the second sampled audio file sounds good, having somewhat "analog-like" quality in it and that's why it can be used in "everyday audio task"
Near every of these "108 dB" PC super audio ADCs have noise level at -72..-75 dB. Slightly better than a P2, but far from advertised "108 dB" which maybe is available in laboratory conditions, but not in the computer at home.
@Ariba said:
Is this not too good to be true?
What have you connected at the ADC inputs?
Good trick to use only a 16 bit range of a 20 or 24 bit signal, and then add the reduced bits in dB later. I get similar results when I try that -> about 108 dB with 20 bits.
I'd done that from the earliest days of testing but never considered building a .wav file could be done so easy. Didn't have the knowledge really. I had partially done text capture for spreadsheet but it long faded from my attention.
Kind of. Like ManAtWork, I'm wanting DC instrumentation, not audio.
I have a battery voltage measurement in the robot. The 24V battery is connected to the P2 pin via 1:10 divider. Then the simply one-line averaging code allowed me to display 5 stable digits of the voltage. Of course the averaging time constant is huge (several seconds) but the 2 kWh battery voltage don't change fast.
And if you play the "sound" of their voltage with extreme amplification it sounds like you hold your ear close to soda water. You can hear the chemistry in the cell working!
Interesting! That really does put the scale into perspective.
Given the noise info presented here, seems to me simple pre-emphasis on capture, along with an appropriate bit depth and sample rate would push the lower frequency noise below -70db.
Either apply post correction in software, or a circuit and get respectable audio back out.
This was done with vinyl, and AM radio, lots of things.
Edit: I see it mentioned, but did not see that while writing...
The 1/f noise character is somewhat similar to the noise introduced by RIAA vinyl record preamps
It's 24-bit sampling using Ariba's code. Then, because I don't know a thing about wave files, the sample data is clipped to 16-bit to fit that format. And because there is basically no signal, the signal itself isn't clipped.
Your posted graph starts at -47 dB at DC end, and goes to -94 dB by about 7 or 8 kHz and finishes a good -95 dB. Not sure how -66 dB fits in there. An improvement of 19 dB?
@pik33 said:
These graphs don't represent anything "absolute": the noise level at the particular frequency depends on FFT length. The more FFT samples, the more subbands, the less energy in one subband and the graph goes lower, while sum of all these subbands energy remains the same.
I got this "silent.wav" signal, converted it to 32 bit using (very old version of) Adobe Audition, and filtered out low and high frequencies. leaving 100..7000 Hz band, to make observation easier. Then I zoomed the waveform. There is 5-bit depth noise in this (sample values from about -16 to 16) and the noise (as sum of all subbands energy) in this band is at about -65 dB level (measured using Audition's level monitoring).
This is consistent with my earlier experiments.
When looking at the spectrum of original, unfiltered "silent.wav" using Audition's scanning and averaging at 65536 FFT samples, the 1/f nature of this noise is easy visible.
While the resulting real resolution is in this case 11 bits, the quality is not like 11-bit digital sampling (which is awful) but rather 16-bit ADC with noise added. The 1/f noise character is somewhat similar to the noise introduced by RIAA vinyl record preamps and 60-something dB SNR is also similar to good analog audio tape or good quality vinyl record. That's why the second sampled audio file sounds good, having somewhat "analog-like" quality in it and that's why it can be used in "everyday audio task"
Near every of these "108 dB" PC super audio ADCs have noise level at -72..-75 dB. Slightly better than a P2, but far from advertised "108 dB" which maybe is available in laboratory conditions, but not in the computer at home.
I removed the click from the silent.wav, highpass filter it at 20 Hz and lowpassfilter at 16kHz and then get the average effective level with the Contrast-tool of Audacity (in the Analyse menu). The result is -74 db
This is only a bit more than 12 bits, but as you say, it's in the region of commercial audio ADCs.
@pik33 said:
... Then I zoomed the waveform. There is 5-bit depth noise in this (sample values from about -16 to 16) and the noise (as sum of all subbands energy) in this band is at about -65 dB level (measured using Audition's level monitoring).
I missed that! The posted FFT graph caught my attention.
So, it would seem then that just looking at the peak-to-peak noise of silence would be another way to calculate ENOB.
From all the information I have built a small test programme.
It turns the input signal into an 18-bit value with a sample rate of 500K.
The 18 bits are shifted to 16 bits.
(I would have preferred a logarithm function here).
The new 16-bit value is then output again by the DAC.
A comparison of the two analogue values shows the quality of the ADC and DAC.
CON
_clkfreq = 256_000_000 ''500kHz * 512
rL = 0 ''audio adc left
pL = 1 ''audio dac left
DAT
org 0
dirl #rL
dirl #pL
wrpin ##P_ADC_1X + P_ADC, #rL
wxpin #%10_1001, #rL ''SINC3 & 18 Bits 512 clocks
wrpin ##P_DAC_990R_3V|P_DAC_DITHER_PWM|P_OE,#pL
wxpin ##512,#pL ''sampelrate in cpu clocks
drvl #rL
drvl #pL
setse1 #%001<<6 + rL
lo waitse1
rdpin smp,#rL ''ADC input 18 Bits
shr smp,#2 ''zu 16 Bits wandeln
wypin smp,#pL ''DAC
jmp #lo
smp long 0
The RDPIN data values of the two "filter" modes, sinc2 and sinc3, are not regular PCM sample data. Coming from the hardware accumulators, it's numerically in an integrated state that still requires differentiation. Here's a diagram of a sinc3 filter for PDM to PCM conversion. Z-1 just means a storage register creating a one cycle delay. MOD_CLK is the ADC bitstream clock, which is prop2 sysclock for an internal ADC. DEC_CLK is regular sampling rate, AKA decimation rate.
I've indicated with red arrow where the prop2 smartpin ends (RDPIN) and software starts. The first stage of differentiation is performed in hardware for free, as there is a trick for performing that without staging. That leaves software to perform the second stage differentiation for sinc2, and additionally another stage for sinc3.
So, to get valid data:
lo waitse1
rdpin smp,#rL ''ADC input 27 bits, log2(512) x 3, 9 x 3
sub smp,diff1
add diff1,smp
sub smp,diff2 'Sinc3
add diff2,smp
zerox smp,#26 ' match to 27-bit hardware accumulators
shr smp,#11 ' 16-bit samples, 27 - 16 = 11
wypin smp,#pL ''DAC
jmp #lo
Oh, the valid full scale range is actually 27-bit + 1. So, a fully positive voltage on the ADC will roll over the differential summing to zero. This can't happen with x1 gain setting. Only x3 or higher gain. If you think it is possible with your hardware then the software workaround is to reduce the sample/decimation period by one. ie: Use WYPIN to set 511 instead of 512.
Comments
Evanh, it's in the /samples/fileserver/ directory. Just copy the spin file into this directory. I just modified an example from this directory for the file server.
Pic18f2550:
Ja, du musst sogar mit 500 kHz abtasten, da sonst das Sinc3 Filter überläuft. Deshalb hab ich in meinem Beispiel so eine tiefe clkfreq gewählt, um überhaupt auf 48 kHz runter zu kommen.
Ich würde 196.608MHz / 512 = 384 kHz wählen, das ist eine Standardfrequenz und der P2 wird nicht so stark übertaktet.
Andy
Hmm, samples/ doesn't exist ...
Here is a copy (with m spin file included). Expand it as sub directory of 'samples' dir.
If you choose other window types and a shorter FFT size, you see some bars at higher frequencies. That's why I don't really trust this frequency analysis results.
If somebody claims 18 or 24 bits of resolution or even accuracy I wouldn't believe him. Somewhere above 16 bits or 100dB SNR things become really complicated and expensive. I worked for a company that develops test equipment for automotive electronics around 2000. One project was to make an A/D converter which offers true 18 bit accuracy from DC to 100kS/s. 18 bits and a +/-10V input means ~80µV resolution and sounds not too hard. But the only way to implement this was to use the best stereo ADC we could get and use one channel for self-calibration and the other for the actual measurement. The ADC, the voltage reference, the multiplexer and all voltage dividers and amplifiers were put in a sealed, heated box regulated to 50°C+/-0.1. For the voltage dividers we had to use several ultra-precision resistors (0.1%, 10ppm/K) in series because a single resistor would drift too much because of self-heating from the current flow. We had to use special protection diodes because the leakage of standard zener or transzorb diodes would cause too much voltage drop in the input lines. And we found out that a $20,000 voltage reference from HP had too much noise. At the end we used normal but temperature controlled alcali batteries calibrated with a precision multimeter. But they had to be brand-new. If you draw 1mA for one second from them they need hours to stabilize, again. And if you play the "sound" of their voltage with extreme amplification it sounds like you hold your ear close to soda water. You can hear the chemistry in the cell working!
24 bits of resolution (~1µV @ 10V range) is possible with heavy low-pass filtering, for example, to monitor strain gauges or thermocouples. But if you need higher bandwidth than a few samples per second it gets really hard.
I downloaded all of Flexprop sources and found it in there. Then fixed another bug in fs9p.cc where it was oddly also not providing a length parameter to strncmp(). Compiled and it works.
Right what I changed is the sample data gain. Since it was just recording silence, it wouldn't clip when when above unity. So I went for x16 gain (20 bits effective) and removed the high four bits so it is still stored as 16-bit samples.
This has the effect of raising the noise floor by 24 dB when analysed:
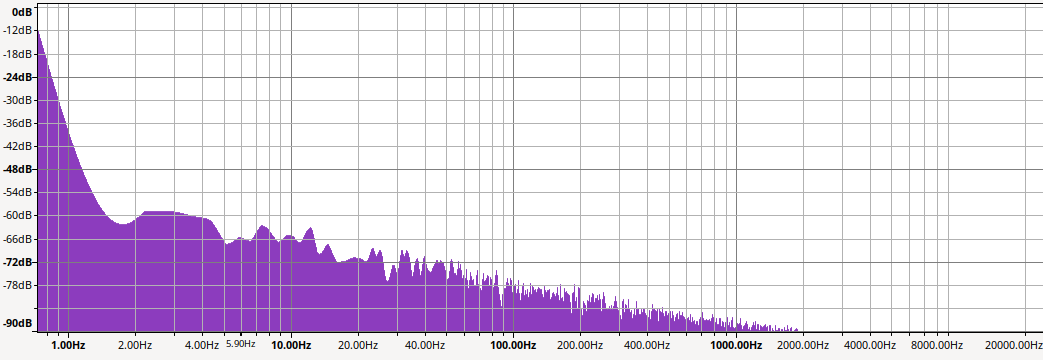
So that graph implies we're getting ENOB >19 above 2 kHz.
And again at x256 gain (24-bit sampling): The waveform first:

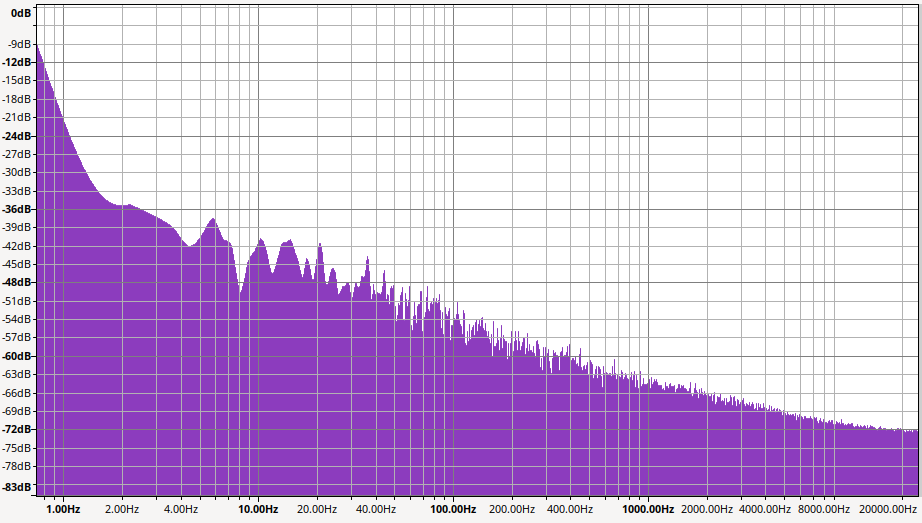
That -72 dB at 20 kHz gets 48 dB subtracted to make it -120 dB (ENOB = 19.6). Best case of course.
And the -36 dB hump (minus 48) is a good match for the -84 dB in the original. Which is still ENOB = 13.6, which is better than I was expecting. I guess that's still not DC though.
BTW, Ariba, I had to tweak
middle long $82_0000For the x256 gain all I did was replace
shr smp,#9 shr smp,#2 'to 16 bitswith
zerox smp, #26 shr smp,#3 ' 24 bitsIs this not too good to be true?
What have you connected at the ADC inputs?
Good trick to use only a 16 bit range of a 20 or 24 bit signal, and then add the reduced bits in dB later. I get similar results when I try that -> about 108 dB with 20 bits.
BTW: a linear freq scale shows it better.
Kind of. Like ManAtWork, I'm wanting DC instrumentation, not audio.
Nothing. Eval Board floating input.
These graphs don't represent anything "absolute": the noise level at the particular frequency depends on FFT length. The more FFT samples, the more subbands, the less energy in one subband and the graph goes lower, while sum of all these subbands energy remains the same.
I got this "silent.wav" signal, converted it to 32 bit using (very old version of) Adobe Audition, and filtered out low and high frequencies. leaving 100..7000 Hz band, to make observation easier. Then I zoomed the waveform. There is 5-bit depth noise in this (sample values from about -16 to 16) and the noise (as sum of all subbands energy) in this band is at about -65 dB level (measured using Audition's level monitoring).
This is consistent with my earlier experiments.
When looking at the spectrum of original, unfiltered "silent.wav" using Audition's scanning and averaging at 65536 FFT samples, the 1/f nature of this noise is easy visible.
While the resulting real resolution is in this case 11 bits, the quality is not like 11-bit digital sampling (which is awful) but rather 16-bit ADC with noise added. The 1/f noise character is somewhat similar to the noise introduced by RIAA vinyl record preamps and 60-something dB SNR is also similar to good analog audio tape or good quality vinyl record. That's why the second sampled audio file sounds good, having somewhat "analog-like" quality in it and that's why it can be used in "everyday audio task"
Near every of these "108 dB" PC super audio ADCs have noise level at -72..-75 dB. Slightly better than a P2, but far from advertised "108 dB" which maybe is available in laboratory conditions, but not in the computer at home.
silent.wav unfiltered spectrum
I'd done that from the earliest days of testing but never considered building a .wav file could be done so easy. Didn't have the knowledge really. I had partially done text capture for spreadsheet but it long faded from my attention.
silent.wav band-pass (100.7000 Hz) filtered waveform, zoomed
I have a battery voltage measurement in the robot. The 24V battery is connected to the P2 pin via 1:10 divider. Then the simply one-line averaging code allowed me to display 5 stable digits of the voltage. Of course the averaging time constant is huge (several seconds) but the 2 kWh battery voltage don't change fast.
Interesting! That really does put the scale into perspective.
Given the noise info presented here, seems to me simple pre-emphasis on capture, along with an appropriate bit depth and sample rate would push the lower frequency noise below -70db.
Either apply post correction in software, or a circuit and get respectable audio back out.
This was done with vinyl, and AM radio, lots of things.
Edit: I see it mentioned, but did not see that while writing...
Pik,
We're definitely improving on the 16-bit limit. Try this ( it's the x256 gain wave file used for my above graph):
That signal (DC filtered) is at about -18 dB
Where this 256x gain came from?
256x gain is 8 bit, 48 dB, so attenuating this signal 256 times gives 18+48=..... 66 dB...
It's 24-bit sampling using Ariba's code. Then, because I don't know a thing about wave files, the sample data is clipped to 16-bit to fit that format. And because there is basically no signal, the signal itself isn't clipped.
Well, the other reason the top 8 bits is tossed is to fit more samples in the hubRAM buffer.
The waveform contains a DC offset. Might want to null that first.
And the first few samples might have a spike too.
Of course I filtered DC off and deleted the spike at the start
If you simply shifted the signal 8 bit left... it doesn't do anything, and that's why 66 dB is still 66 dB.
All good. Just making sure.
Your posted graph starts at -47 dB at DC end, and goes to -94 dB by about 7 or 8 kHz and finishes a good -95 dB. Not sure how -66 dB fits in there. An improvement of 19 dB?
I think all the filtering is just for noise reduction, and have a negative effect on speed.
How high are the noise levels?
Does P_ADC_1X deliver the measured value fastest?
Why don't you use several smartpins at the same time for one signal?
e.g. 4 Smartpinns add all results and divide by 4. could this be faster?
I removed the click from the silent.wav, highpass filter it at 20 Hz and lowpassfilter at 16kHz and then get the average effective level with the Contrast-tool of Audacity (in the Analyse menu). The result is
-74 dbThis is only a bit more than 12 bits, but as you say, it's in the region of commercial audio ADCs.
I missed that! The posted FFT graph caught my attention.
So, it would seem then that just looking at the peak-to-peak noise of silence would be another way to calculate ENOB.
From all the information I have built a small test programme.
It turns the input signal into an 18-bit value with a sample rate of 500K.
The 18 bits are shifted to 16 bits.
(I would have preferred a logarithm function here).
The new 16-bit value is then output again by the DAC.
A comparison of the two analogue values shows the quality of the ADC and DAC.
CON _clkfreq = 256_000_000 ''500kHz * 512 rL = 0 ''audio adc left pL = 1 ''audio dac left DAT org 0 dirl #rL dirl #pL wrpin ##P_ADC_1X + P_ADC, #rL wxpin #%10_1001, #rL ''SINC3 & 18 Bits 512 clocks wrpin ##P_DAC_990R_3V|P_DAC_DITHER_PWM|P_OE,#pL wxpin ##512,#pL ''sampelrate in cpu clocks drvl #rL drvl #pL setse1 #%001<<6 + rL lo waitse1 rdpin smp,#rL ''ADC input 18 Bits shr smp,#2 ''zu 16 Bits wandeln wypin smp,#pL ''DAC jmp #lo smp long 0The RDPIN data values of the two "filter" modes, sinc2 and sinc3, are not regular PCM sample data. Coming from the hardware accumulators, it's numerically in an integrated state that still requires differentiation. Here's a diagram of a sinc3 filter for PDM to PCM conversion. Z-1 just means a storage register creating a one cycle delay. MOD_CLK is the ADC bitstream clock, which is prop2 sysclock for an internal ADC. DEC_CLK is regular sampling rate, AKA decimation rate.
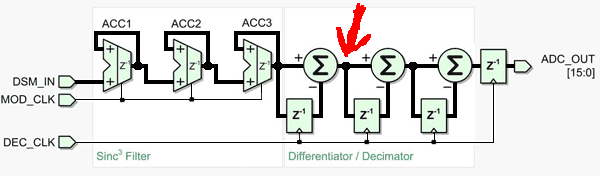
I've indicated with red arrow where the prop2 smartpin ends (RDPIN) and software starts. The first stage of differentiation is performed in hardware for free, as there is a trick for performing that without staging. That leaves software to perform the second stage differentiation for sinc2, and additionally another stage for sinc3.
So, to get valid data:
lo waitse1 rdpin smp,#rL ''ADC input 27 bits, log2(512) x 3, 9 x 3 sub smp,diff1 add diff1,smp sub smp,diff2 'Sinc3 add diff2,smp zerox smp,#26 ' match to 27-bit hardware accumulators shr smp,#11 ' 16-bit samples, 27 - 16 = 11 wypin smp,#pL ''DAC jmp #loOh, the valid full scale range is actually 27-bit + 1. So, a fully positive voltage on the ADC will roll over the differential summing to zero. This can't happen with x1 gain setting. Only x3 or higher gain. If you think it is possible with your hardware then the software workaround is to reduce the sample/decimation period by one. ie: Use WYPIN to set 511 instead of 512.