Iterative binomial filter in Spin
 Phil Pilgrim (PhiPi)
Posts: 23,514
Phil Pilgrim (PhiPi)
Posts: 23,514
I'm working on a Propeller app that involves the smoothing of time-series data. One method that's often used for this is the very simplistic exponential averaging:
The closer p is to 1, the more smoothing you get. In physical terms, this is equivalent to a simple RC filter and is a type of infinite impulse response (IIR) filter. This means that, theoretically, a datum an infinite time in the past still affects the current average. Of course, due to rounding and truncation in computer math, the effect is finite, but can be quite long.
Another type of filter is the boxcar smoother:
This is a form a of a finite impulse response [FIR] filter, in that the influence of any particular datum lasts only n times in the data stream. It's not a very nice filter, because it has some nasty bumps at the high end of its frequency response.
A binomial filter is like a boxcar smoother, except that the past values are not all weighted the same. In fact, they're weighted by the numbers in one of the odd lines in Pascal's triangle, and divided by the sum, which is always a power of two:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
The further down the triangle you go, the larger the coefficients become, to the point where overflow is a real problem when they're used to multiply the data points. So what I've done is to apply just the [1, 2, 1] filter to the data iteratively n times to get to the nth odd row of the triangle. And this just involves adding and shifting at each step.
To do this, the program uses a history array 3*n longs long. Each successive triad contains the history of the last three data points, where the data in triad i are the results of applying the [1, 2, 1] filter to triad i-1. I have sat down with pencil and paper to prove that doing this twice (n = 2) is equivalent to applying the [1, 4, 6, 4, 1] filter. So by extrapolation, I'm assured that successive odd rows fall out from further operations. The downside to doing it this way is the increased likelihood of truncation errors. But that's the price to be paid for no overflows.
Here's the program:
This uses a 30th order binomial filter, which, if done explicitly, would involve 59 coefficients. I plotted the data it output in Excel. Here's the graph:
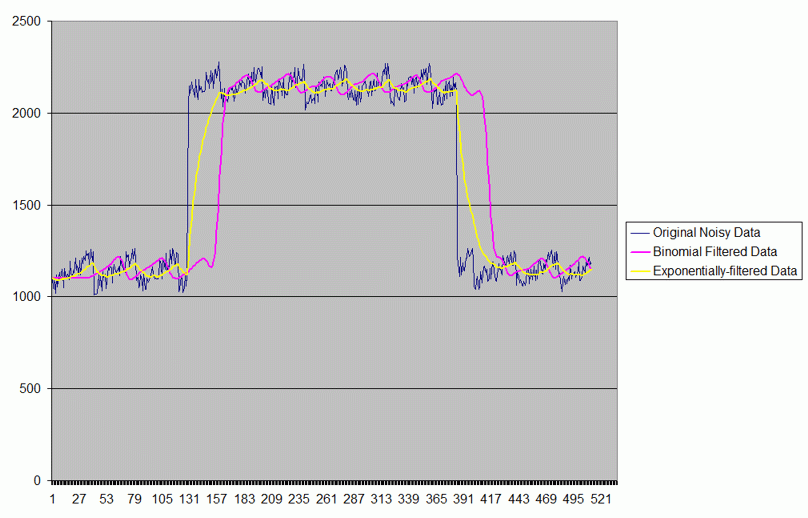
The major takeaways are these:
-Phil
avgi = avgi-1 * p + data * (1 - p), where 0 < p < 1
The closer p is to 1, the more smoothing you get. In physical terms, this is equivalent to a simple RC filter and is a type of infinite impulse response (IIR) filter. This means that, theoretically, a datum an infinite time in the past still affects the current average. Of course, due to rounding and truncation in computer math, the effect is finite, but can be quite long.
Another type of filter is the boxcar smoother:
avg = (xi-n+1 + xi-n+2 + ... + xi-1 + xi) / n
This is a form a of a finite impulse response [FIR] filter, in that the influence of any particular datum lasts only n times in the data stream. It's not a very nice filter, because it has some nasty bumps at the high end of its frequency response.
A binomial filter is like a boxcar smoother, except that the past values are not all weighted the same. In fact, they're weighted by the numbers in one of the odd lines in Pascal's triangle, and divided by the sum, which is always a power of two:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
The further down the triangle you go, the larger the coefficients become, to the point where overflow is a real problem when they're used to multiply the data points. So what I've done is to apply just the [1, 2, 1] filter to the data iteratively n times to get to the nth odd row of the triangle. And this just involves adding and shifting at each step.
To do this, the program uses a history array 3*n longs long. Each successive triad contains the history of the last three data points, where the data in triad i are the results of applying the [1, 2, 1] filter to triad i-1. I have sat down with pencil and paper to prove that doing this twice (n = 2) is equivalent to applying the [1, 4, 6, 4, 1] filter. So by extrapolation, I'm assured that successive odd rows fall out from further operations. The downside to doing it this way is the increased likelihood of truncation errors. But that's the price to be paid for no overflows.
Here's the program:
CON
_clkmode = xtal1 + pll16x
_xinfreq = 5_000_000
MAXSTAGES = 50
UNDEF = $8000_0000
VAR
long history[MAXSTAGES * 3]
OBJ
pst: "Parallax Serial Terminal"
PUB start | seed, yy, zz, i, base, avg
pst.start(9600)
configure_smoothing(@history)
repeat i from 0 to 511
if (i > 128 and i < 384)
base := 2000 '+1000 pulse in the middle.
else
base := 1000
yy := base + (?seed >> 25) + (i // 40) * 4 'Apply noise and sawtooth wave to signal.
zz := smooth(@history, yy, 30) 'Do a 30-stage binomial smoothing.
if (i)
avg := (avg * 11 + yy) / 12 'Exponential smoothing for comparison.
else
avg := yy
pst.dec(yy)
pst.char(" ")
pst.dec(zz)
pst.char(" ")
pst.dec(avg)
pst.char(13)
'The following two subroutines set up and perform the binomial smoothing operation.
PUB configure_smoothing(hist_addr)
long[hist_addr] := UNDEF 'Constant used for undef, since Spin doesn't have one.
PUB smooth(hist_addr, value, n) | i
n += n << 1 'Multiply n by 3.
if (long[hist_addr] == UNDEF ) 'If first value, fill history with it.
longfill(hist_addr, value, n)
return value
else
longmove(hist_addr, hist_addr + 4, n - 1) 'Otherwise shift history left by one long.
repeat i from 0 to n - 1 step 3 'Iterate the [1 2 1] filter.
long[hist_addr][i + 2] := value 'Insert value as last in local history triad.
value := (long[hist_addr][i] + (long[hist_addr][i + 1] << 1) + value + 3) >> 2 'New value := (value[i - 2] + 2 * value[i - 1] + value[i]) / 4
return value
This uses a 30th order binomial filter, which, if done explicitly, would involve 59 coefficients. I plotted the data it output in Excel. Here's the graph:

The major takeaways are these:
1. Both the exponential and binomial filters do a good job of cleaning up short-term fluctuations in the data.
2. The binomial filter does a much better job following data trends that the exponential filter mushes up.
3. The binomial filter entails a delay equal to n. The reason for this is that the highest coefficient is in the middle, n-1 data samples in the past from the current one. Another way to look at it is that the binomial filter considers not only the current value and values in the past, but also values in the future to compute the smoothing.
2. The binomial filter does a much better job following data trends that the exponential filter mushes up.
3. The binomial filter entails a delay equal to n. The reason for this is that the highest coefficient is in the middle, n-1 data samples in the past from the current one. Another way to look at it is that the binomial filter considers not only the current value and values in the past, but also values in the future to compute the smoothing.
-Phil


Comments
Its a bit less computational load to use [1 1] as the basis, rather than [1 2 1], twice as many
steps but only 2 x (move + add) rather than 3 x move + shift + add + add.
The moves can be eliminated by ping-ponging between two copies, some Python to
illustrate (this ought to translate to two unrolled PASM loops, one for each value of sense, meaning
cost is mainly one add instruction per [1 1] stage.)
N = 16 state = np.zeros ([2, N], float) sense = 0 def smooth (inp): global sense state [sense, 0] = inp for i in range (N-1): state [sense, i+1] = state [0, i] + state [1, i] out = state [0, N-1]+state [1, N-1] sense = 1 - sense # swap columns return out / (1 << N)Here's the raw data generated by the above program:
-Phil
-Phil
Mike R.
Here is a 4th order delta filter ...
The superimposed image at the bottom with the spike going down on the left and up on the right is the delta between Samples.
The Sample starting at about 1000 is the original data.
The proceeding samples represent each successive order of filtering. I purposefully offset the Y by 250 on each filter.
The filter consists of a FIFO window of three samples, call them A1, A2, and A3. D1,D2,and D3 are Delta values. F1 is the Filtered output. Each pass of the filter, you lose the last two data samples.
D1 = A1-A2
D2 = A1-A3
D3 = INT((D1+D2)/2)
F1 = A1-D3
So,
D3 = (D1 + D2) / 2 = (A1 - A2 + A1 - A3) / 2 = A1 - (A2 + A3) / 2
F1 = A1 - D3 = (A2 + A3) / 2
This looks like the [1, 1] kernel, but peering into the future, rather than into the past, which explains the increasing negative delay with each pass. Right?
-Phil
Peering into the future is correct I guess, although technically you are still looking at the past since you lose the last two data points or they become part of the equation rather for each Delta order you implement. The idea is that you need at least 3 data points in a first in first out approach, so the output data for each order isn't valid until you have read at least 3 points, either way you lose the last two or first two depending on how you look at the incoming data stream. For the 4th order Delta you end up losing 8 data points.
Here is the same data taken to an 8th order Delta filter. 16 data points are lost at the end so the 512 data set is now 496
EDIT: losing 2 data points per order probably isn't correct. A Phase shift or delay would be more accurate. SO for each time you implement a filter stage, you introduce a delay of two samples per stage
-Phil
When it comes to filter the data, the question always is, what do you expect to happen. This sample data seems artifical, as there is a pulse, a sawtooth and noise. If you look to the derivative, Beau created, it is obvious, there are spikes in a certain distance and at certain amplitude, so these can be predicted to and seen as a part of the signal. It is a good idea to not filter those spikes out. So one could say: calculate derivative, limit amplitude to a level 3 sigma, apply a filter and remove the filtered out components from the original signal, that should suppress the noise and keep the information.
In this signal, the question is: what is the information. Is it every new sample or is the information only valid after a sawtooth completed? In the last case, the value is the average over one sawtooth and you have a time delay of 1/2 period anyway. In the other case, the history tells you, there is a systematical sawtooth and the new sample just tells you, if this sawtooth continues or ends. Such deviations can only be found, when the noise is less then the change of the signal.
F1 = (A2 + A3) / 2
F2 = (A3 + A4) / 2, etc.
And that's the same as Mark_T's technique for iterating the binomial filter, at least after any even number of iterations. (If you stop at an odd number, you don't get a true binomial filter.)
Ideally, the filter I use, would look something like this:
fi = f(a0*xi + a1*xi-1 + ... + an*xi-n)
The binomial filter fits the bill. But, because the middle a terms are the largest ones, they contribute to a large phase delay. What I propose is to come up with a binomial filter whose left tail is applied to past values, the center term to the current value, and the right tail to "future" values extrapolated from past values, using a polynomial or other regression technique. That way, the phase delay is minimized.
-Phil
What we actually do when applying a filter, we write one vector of lenght 1 with the n components being the filter coefficients and then we take the last n samples of the signal as a second vector and we calculate the scalar product to get "how much" of the filter vector is "in" the signal.
Imagine the signal is constant but noisy. Then the scalar product to the middle of the binominal is just 50%. This will eliminate the noise and not introduce a phase shift, as the signal is constant, so phase shift doesn't apply. This will also work for any filter coefficients. The binomial just weights the values close to the center a little more, so if the signal is not constant, your result will be closer to the actual value of the last sample. If you could look into the future and see, that the signal is symmetrical to the past, then the next 50% of the signal will show the same value as the first 50%. But as we do not know, how the signal develops this is just lotterie.
So you could do this experiment: take 50% of the binominal and calculate the current value. Next: take 70% of the binominal, so the peak is in the past, and calculate the current signal. Now imagine to go back in time to the max of 70 %, predict what will happen 20% later, actual the known current value and determine, if you prediction was right. Then, as you know the error you made, assume that you just now made the same error and correct it.
That is just the basic principle how to make a learning system. But, always look that your predictions don't hurt conservation of momentum and energy. Or, to bring a less abstract example: if your employment rate raises constantly, there is a natural limit of 100 %. If someone tells you, that growth will continue for ever, he might be false.
Sounds like a recipe for a nonlinear chaotic system to me... And you lose all the predictable
properties of a time-invariant linear system.
In the future we will have P2 that is for sure, in the past, we had no P2, that's for sure to. And in between, we wait.....
No!!! That's precisely what I'm trying to get away from. I'm totally committed to the FIR approach. I just need something without a huge phase lag that I can explain to my customer.
-Phil
Calculating the derivative, but D(i) = S(i) - S(i-2)
The idea behind that is: obviously, the steps in the signal (red) extend over more than one sample and so highest frequency noise (alternating) is suppressed, while the signal steps are not. By differentiation, the constant part is lost, so this part has to be added separately when reintegrating.
Integration now takes every difference, so the result has to be devided by 2 (green). To improve noise suppression, the derivative can also be averaged (in this case (d(i)+d(i-1)+d(i-2))/3 which shows the result in red.
It looks that the key with filtering is to know, what you are looking for. So if you look to your neighbor and you see a mob, take care that your sight was not filtered by a mirror.
Then you have to put up with a small number of coefficients in the FIR - have you tried approximations to sinc()
using small integer coefficients (mainly powers of two) - for instance:
[1, 2, 1, 0, -2, -4, -2, 0, 4, 12, 16, 18, 16, 12, 4, 0, -2, -4, -2, 1, 2, 1]
Which has a cutoff of about fs/8 and latency of 10 samples - derived by adhoc means. I don't know how to
determine FIR coefficients for minimum phase, other than to simply truncate the future coefficients sooner.
http://dspguru.com/files/cic.pdf and https://www.embedded.com/design/configurable-systems/4006446/Understanding-cascaded-integrator-comb-filters
Outside of the use for decimation and interpolation, an integrator-comb filter is another way of looking at
boxcar filtering as a combination of an integrator and a comb filter where the integrator pole cancels a single
zero of the comb filter.
high-precision-propeller-sigma-delta-adc
And here's a pdf link to that nice article by Richard Lyons:
https://faculty-web.msoe.edu/prust/sdr/cic_filters.pdf
One thing I've discovered the hard way is that so much in the filtering world is applicable to AC signals (e.g. audio, RF) only, neglecting the DC component. I thought maybe I could use my FIR filter generator to come up with a filter for the time-series data. But no. Even though the TFilter FIR filter design tool claims a gain of 1.0 for a low-pass filter, the gain at 0 Hz can be less than that, which means the filtered data will be skewed downwards. This is because the ripple in the passband may not intersect the Y-axis at 0 dB.
The simplest way to guarantee DC unity gain is to make sure that all of the FIR filter coefficients sum to 1.0. If they are all positive, so much the better. This is not the case with many TFilter-generated filters, even though the AC gain is still 1.0.
Currently, I'm looking at a combination of a causal FIR filter (i.e. one with minimum phase delay), followed by median filtering.
-Phil
-Phil
The most simple assumption is: noise is stochastic. In this case the filter of choise is the gaussion scaled sliding average. If noise is created by accident, then it shouldn't make any difference, which sampling points you take. But as there is a underlying signal, selecting the sampling points matters. So anyway you have to have a model of the signal generating mechanism.
Chopping the signal works well, to bring the signal from DC up to a set higher frequency where it can be dealt with in an exquisite narrowband filter. Unfortunately a lot of those environmental signals can't be chopped in a way that doesn't include the interference.