@Rayman said:
Curious of the cog's streamer Goertzel mode would be useful here...
I've been getting the impression that, though it a tantalizing option being named Goertzel and all, that that streamer mode deals well with high frequencies but not low.
plenty of options to work through. time to sort some of them out and compare the results.
@cgracey said:
Ganging ADC pins can improve conversion quality, but it is not necessary.
in this case, the strategy I'm going for is not to to get better quality signal or even a faster calculation of FFT (I'm not one to invent new math)
but, by beginning sample set of values for a determined-to-be-effective set of FFT data (say 4096 samples) on one of 4 cogs (in round-robin fashion) every 23ms until the first one finds the frequency, which, depending on when the successful detection occurred, may be approaching 96ms sooner than only FFTing consecutively on a single cog.
... as @SaucySoliton indicates here
just how long does it take to complete and FFT o 4096 samples at 300MHz P2 clock?
actually, if the FFT takes less time than 23ms, then just continual consecutive FFT with a sliding window of 4096 samples over the datastream could do just as well...
no matter how fast the FFT can be, doing more concurrently can shift the discovery of a frequency earlier in actual wall clock time- and that is the goal.
Perhaps you could just use a period-measurement smart pin mode and select one of the digital-filtering modes for it. If the fundamental is very strong, that could do the trick.
I'll look deeper in here, too. I didn't realize it had inbuilt filters.
the extent of the challenge: identify, as soon as possible, the presence of one of 6 fundamental frequencies... which may, or may not, be there at any given instant. leave it at that.
I'll point out the critical, though seemingly minor, distinction between "as soon as possible" and "as fast as possible"
I'm not looking/expecting/hoping to bend math and physics. I'm simply meaning to bring to bear the huge amount of concurrent processing power within 8 P2 cogs and the SmartPins themselves, each working in concert together and each beginning at consecutive small intervals, to arrive at a result as soon (in wall clock time) as possible, no faster at all than math/physics dictate.
That said: solving your problem will imply a huge progress in signal processing, comparable to Fourier's fundamental work, I guess.
It is @cgracey (and Parallax team) that deserves all the credit for delivering such a fantastic digital toolbox on such low power.
I'm not looking/expecting/hoping to bend math and physics.
Good starting point. In doing a FFT it is very often not recognized, that the selection of the interval determines the frequency spectrum. A sinoid that fits 10 times into the interval will result in a single value for frequency 10. A sinoid that fits 10.3 times into the interval will still show the largest value at 10 Hz, but all the other frequencies will be non-zero.
If you have a single period of 10 Hz in a one second interval you will see dominant value at 10Hz, but depending on the position in the interval the phase will change.
What I want to show: a fourier transform is the wrong way to go, independent of the computational power. A FIR filter could be more appropriate. Which also can make use of the parallel processing power.
@ngeneer said:
just how long does it take to complete and FFT o 4096 samples at 300MHz P2 clock?
actually, if the FFT takes less time than 23ms, then just continual consecutive FFT with a sliding window of 4096 samples over the datastream could do just as well...
no matter how fast the FFT can be, doing more concurrently can shift the discovery of a frequency earlier in actual wall clock time- and that is the goal.
Perhaps you could just use a period-measurement smart pin mode and select one of the digital-filtering modes for it. If the fundamental is very strong, that could do the trick.
I'll look deeper in here, too. I didn't realize it had inbuilt filters.
For a 4096 FFT it will theoretically take 4.8x longer than a 1024. If we can use Chip's pasm FFT, then a 4096 should take 14.4mS.
The "acquisition time" is the time it would take to fill the input buffer with audio samples. The effective latency might only be half or 3/4 of this. It's physically unavoidable. You must observe the string for long enough to be certain of the frequency.
If I was writing this code, here is what I would try first:
1. Precompute sine/cosine waves for the frequencies of interest. Apply a windowing function so we don't have to apply the window function to the audio data. The table for each frequency could be from 1024 to 2048 samples of complex data. 98kB ram
2. Audio samples are captured and written into a circular buffer of maybe 4096 length. 16kB ram
3. 6 cogs in parallel do multiply and accumulate between samples of audio data and the Goertzel table data. With careful timing the accumulation would be complete just after the last audio sample used was written to memory.
4. Compare the Goertzel accumulation results to decide if and which note was played.
Step 3 can be started often, with much less than 1024 new samples of audio data. This makes for overlapping Goertzel samples. Compute time should be <1mS. Maybe 6 cogs is overkill there. Most of the latency would just be waiting for new audio samples to work their way through the input buffer.
@ErNa said:
Good starting point. In doing a FFT it is very often not recognized, that the selection of the interval determines the frequency spectrum. A sinoid that fits 10 times into the interval will result in a single value for frequency 10. A sinoid that fits 10.3 times into the interval will still show the largest value at 10 Hz, but all the other frequencies will be non-zero.
If you have a single period of 10 Hz in a one second interval you will see dominant value at 10Hz, but depending on the position in the interval the phase will change.
What I want to show: a fourier transform is the wrong way to go, independent of the computational power. A FIR filter could be more appropriate. Which also can make use of the parallel processing power.
That's why generally, a windowing function is applied before performing an FFT (and to compensate, the end of one transform overlaps the beginning of the next). That's also not perfect, but gets rid of the hard cut-off at the edges.
That's why generally, a windowing function is applied before performing an FFT (and to compensate, the end of one transform overlaps the beginning of the next). That's also not perfect, but gets rid of the hard cut-off at the edges.
Windowing is well known, but in the end it doesn't change anything but the signal. The point is: you can select an interval just because this interval's signal is periodical over all time. A window function brings down the signal close to the intervals ends and so forces continuation. But the price you have to pay is: you can see the signal as a carrier and the window function as a modulation, so this window function will create side bands to the carriers frequencies.
What is not known in the broad audience: the FFT is fastest when the interval's length is of 2^N, but you can also use it on signals of length 1.5 * 2^N with slightly increased runtime, the same is true for arbitrary lengths. So if you know the "real" fundamental you can select an interval of this length. Imagine you have a 1.024 second period, then 1024 samples will result in a single frequency amplitude >0. If the period is 1.1 seconds, you will see a broad spectrum. So you could iterate to find the interval that creates the spectrum of most simple complexity.
But this will not run in real time :-)
Once Fourier found a way to represent the temperature distribution on a rod by approximation of harmonic functions. And describe the cooling process by amplitudes of frequencies. There was a long way to find a linkage to e.g. group theory https://en.wikipedia.org/wiki/Fourier_transform_on_finite_groups
Fourier Transform is a universe still not fully understood.
Imagine: The FT shows you it there is a periodical behavior in a signal. Every signal is defined by (equidistantly) sampled values. The task of the FT is to find a more simple representation of this signal, we call spectrum. So we could define: a signal is non periodical, if the fourier transform is of same complexity. So a Gaussian for sure is not periodical and the FT again is a Gaussian. It's called an "Eigenfunktion" of the FT. Linear algebra allows to find many more Eigenfunktions.
We just see the tip of an ice berg!
Happy New Year!
P.S.: I do not understand the theory in the linked article, I just realize: there is more to learn.
@ErNa said:
... A sinoid that fits 10 times into the interval will result in a single value for frequency 10. A sinoid that fits 10.3 times into the interval will still show the largest value at 10 Hz, but all the other frequencies will be non-zero.
If you have a single period of 10 Hz in a one second interval you will see dominant value at 10Hz, but depending on the position in the interval the phase will change.
What I want to show: a fourier transform is the wrong way to go, independent of the computational power. A FIR filter could be more appropriate. Which also can make use of the parallel processing power.
It doesn't matter what algorithm you use. You can't fool the laws of nature. A reciprocal frequency counter (measuring the period and calculate f=1/p) works only if you have a single, pure fundamental frequency. As soon as you have harmonics, noise or a mix of several frequencies that distorts the zero crossings or trigger points of your timer, cause jitter and therefore makes the result inaccurate.
If you do an FFT you effectively serach for the highest amplitude in the frequency domain. To get enough resolution you have to sample multiple periods of the signal. As I said earlier resolution is inversely proportional to the sampling window time. To distinguish between 100 and 110Hz you have to sample at least 10 periods.
Same for FIR filters. The higher the order of the filter or the sharper the cutoff the longer the group delay has to be. This means: longer buffer and more taps and therefore more time until you get the result.
There is no way around this unless you have an oracle machine or a crystal ball chip that can look into the future.
That's a challenge, what is the relative signal level of the desired signal, amongst other signals ? If you can mic the instrument of interest itself, things will be easier.
You may need to use envelope information, as well as frequency information.
A 82-110Hz bandpass would help S/N challenges, but it would mask the envelope information so separate envelope and signal filter paths could be helpful at the experiment stage.
I'd build those externally in analog with scope triggers, for the experiment stage, and then you can do Sw filters later.
6 Envelope triggered auto-correlators might manage this ?
All good comments. thanks.
Certainly there will be experimentation on the bench and in the field. There is plenty of research and suggestions on the fast part, the fast-as-possible-part will need some actual testing and comparison. It may come to mic'ing them directly.
I would start with direct mic'ing, and see if a combination of envelope sense for the trigger and ringing sense for the frequency can be good enough.
This is a very focused problem, so you could capture 40ms of waveforms, then run a best-match compare against 6N stored examples.
If you hope to fast-sense 6 bands, from 82~110Hz, that's going to need jitter/out of band disturbances under 2-3% - sounding tough, even with direct mic'ing.
How narrow do you need the detect ? eg if a frequency is exactly half way between two bins, what should happen ?
Is this a which-one single impulse frequency problem, or do you hope to have any-of-6 arrive, at any phase ?
What is needed is some kind of reporting in real time that alerts to advents in the signal. I don't know how to make this, but I can imagine what its output would look like: Messages about the signal as it changes, which would include harmonic information.
@Mickster and, a little more searching turned this up https://www.vguitarforums.com/smf/index.php?topic=21469.0
maybe there is a bit of a vacuum now in that tiny market to do it "better" (which may only mean, "more cost effective") with other unique features.
here is an interesting quote from 2011 article when Antares we being embedded in guitar,,,and how they simplified the detection dsp with individual pickups on each string... "The hex has been around for a while, but it’s a big deal to use it in this way for guitarists since you don’t need to try to do any polyphonic pitch recognition. Literally direct note access. Also, signals add nonlinearly, so effecting each string individually has a different sound than doing emulation on the mix." https://cdm.link/2011/05/auto-tune-for-guitars-doesnt-have-to-be-like-auto-tune-for-vocals-the-digital-guitar-future/
wasn't really what I was going for. but all very interesting.
Knowing all-too-well what luddites/snobs/purists, guitarists tend to be; I saw the writing on the wall and so I snapped-up three of these guitars. Just recently, I came across another new-in-box and so now I have four.
Been through the mill for half-a-century (playing guitar) and have had all the big-name stuff but these Peavey AT-200s are keepers.
Only one of mine has the "full-pack" but I found someone who knows how to rip it and transfer it to my other three.
Sooo many guitarists regret not buying the AT-200 but the marketing was less than half-hearted. The big stores would never have one hanging on the wall because they didn't want to sell a guitar that could do the work of three or more guitars. They want the snobs to spend thousands on a piece of fancy furniture that cannot possibly compete with the AT-200's perfect intonation. Can you imagine the "WTF" looks I get from other guitarists when I switch to an open-tuning in mid song
The Headrush only has the vocal Autotune which I detest
Jam Origin polyphonic pitch recognition is pretty darned amazing. Took a few hours to get the hang of but it opens-up a whole new world. I use a puny Windows PC and the CPU doesn't seem to take much of a hit.................Would be a dream-come-true if the P2 could handle these tasks
If there was a way to do something like a Goertzel for a single frequency, plus all of its harmonics, that would be great. It would be a pitch detector, then. Twelve of those could cover the musical scale.
Twelve FFTs could do this, too. I guess I kind of asked for an FFT above.
If there was a way to do something like a Goertzel for a single frequency, plus all of its harmonics,
this is kinda the approach I think will serve best in my situation at the moment.
I'm not that fast and practiced with Propeller dev to wing off an experiment or three in an evening. but, I'm more and more appreciating Spin and the development and set of delivered libraries with the PropellerTool... all much more clear what was the set of essential libraries to access the essential features of the SmartPins. Coming at Propeller development from a non-Windows world has confounded my Propeller effectiveness more than I care to think about... I've come further at being effective in the past week since I've succumbed to running a Windows machine to have access to the official supported tools. That is not to be a knock on any of the tremendous community efforts at other language/OS support for Propeller. In fact I contribute to some Patreons for they have allowed me to even experience the Propeller at all in the last year. I fully realize the essential value of the community contributions to the Propeller effort.
that was a tangent, but a developer experience I thought should get back to Parallax that maybe will help somewhere. Now I'll be more effective, and understand what I was missing coming into this community, maybe I can be a more effective contributor to help others in through what ever language/OS they're coming from.
I plan to have more focused time this weekend to do some actual code/hardware explorations and report back to this thread.
@cgracey said:
If there was a way to do something like a Goertzel for a single frequency, plus all of its harmonics, that would be great. It would be a pitch detector, then. Twelve of those could cover the musical scale.
Twelve FFTs could do this, too. I guess I kind of asked for an FFT above.
I don't think that you need too many harmonics for a string instrument. A properly tuned Guitar starts at 82 Hz and has 4 octaves. Add one for harmonics that's 60 frequencies up to 1312Hz, needing 2624 Hz sample frequency. At 200MHz clock you have 76k cycles between 2 samples.
Software Goertzel with 32*16.16 multiply needed about 125 cycles per frequency and sample, so one cog can handle all frequencies.
More than one cog can be used to start analysing in a hunting manner.
It's late, this seems to be too easy?
If there was a way to do something like a Goertzel for a single frequency, plus all of its harmonics,
I plan to have more focused time this weekend to do some actual code/hardware explorations and report back to this thread.
so, feeling my way 'round Spin2 and getting electret mic setup and trying assorted tone generation methods through a small amplified speaker on the bench... I figured I'd setup a little routine that "listened" on one core while I played assorted tones on and around the target frequency just to get a handle on methods of audio frequency detection. here is the ADC signal heard through the electret, noting all the crunchy sound of NCO tone generation on a speaker cone of dubious quality:
Now, it is time I go this mystical software Goertzel algorithm function
Comments
Curious of the cog's streamer Goertzel mode would be useful here...
If you only need six frequencies, maybe there's enough cogs?
Guessing more efficient to just do many Goertzel calculations in assembly though....
I've been getting the impression that, though it a tantalizing option being named Goertzel and all, that that streamer mode deals well with high frequencies but not low.
plenty of options to work through. time to sort some of them out and compare the results.
in this case, the strategy I'm going for is not to to get better quality signal or even a faster calculation of FFT (I'm not one to invent new math)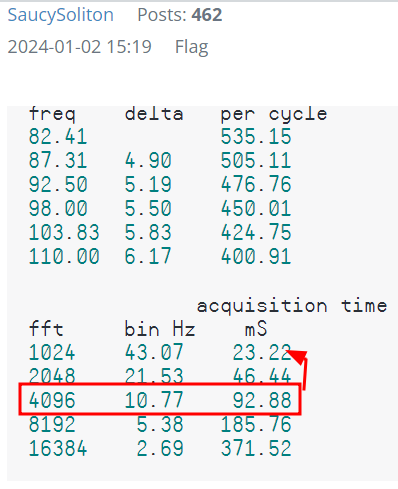
but, by beginning sample set of values for a determined-to-be-effective set of FFT data (say 4096 samples) on one of 4 cogs (in round-robin fashion) every 23ms until the first one finds the frequency, which, depending on when the successful detection occurred, may be approaching 96ms sooner than only FFTing consecutively on a single cog.
... as @SaucySoliton indicates here
just how long does it take to complete and FFT o 4096 samples at 300MHz P2 clock?
actually, if the FFT takes less time than 23ms, then just continual consecutive FFT with a sliding window of 4096 samples over the datastream could do just as well...
no matter how fast the FFT can be, doing more concurrently can shift the discovery of a frequency earlier in actual wall clock time- and that is the goal.
I'll look deeper in here, too. I didn't realize it had inbuilt filters.
I'll point out the critical, though seemingly minor, distinction between "as soon as possible" and "as fast as possible"
I'm not looking/expecting/hoping to bend math and physics. I'm simply meaning to bring to bear the huge amount of concurrent processing power within 8 P2 cogs and the SmartPins themselves, each working in concert together and each beginning at consecutive small intervals, to arrive at a result as soon (in wall clock time) as possible, no faster at all than math/physics dictate.
It is @cgracey (and Parallax team) that deserves all the credit for delivering such a fantastic digital toolbox on such low power.
Good starting point. In doing a FFT it is very often not recognized, that the selection of the interval determines the frequency spectrum. A sinoid that fits 10 times into the interval will result in a single value for frequency 10. A sinoid that fits 10.3 times into the interval will still show the largest value at 10 Hz, but all the other frequencies will be non-zero.
If you have a single period of 10 Hz in a one second interval you will see dominant value at 10Hz, but depending on the position in the interval the phase will change.
What I want to show: a fourier transform is the wrong way to go, independent of the computational power. A FIR filter could be more appropriate. Which also can make use of the parallel processing power.
For a 1024 FFT in C: ~16mS https://forums.parallax.com/discussion/comment/1503890/#Comment_1503890
For a 1024 FFT in pasm: 3mS https://forums.parallax.com/discussion/170948/1024-point-fft-in-79-longs/p2
For a 4096 FFT it will theoretically take 4.8x longer than a 1024. If we can use Chip's pasm FFT, then a 4096 should take 14.4mS.
The "acquisition time" is the time it would take to fill the input buffer with audio samples. The effective latency might only be half or 3/4 of this. It's physically unavoidable. You must observe the string for long enough to be certain of the frequency.
If I was writing this code, here is what I would try first:
1. Precompute sine/cosine waves for the frequencies of interest. Apply a windowing function so we don't have to apply the window function to the audio data. The table for each frequency could be from 1024 to 2048 samples of complex data. 98kB ram
2. Audio samples are captured and written into a circular buffer of maybe 4096 length. 16kB ram
3. 6 cogs in parallel do multiply and accumulate between samples of audio data and the Goertzel table data. With careful timing the accumulation would be complete just after the last audio sample used was written to memory.
4. Compare the Goertzel accumulation results to decide if and which note was played.
Step 3 can be started often, with much less than 1024 new samples of audio data. This makes for overlapping Goertzel samples. Compute time should be <1mS. Maybe 6 cogs is overkill there. Most of the latency would just be waiting for new audio samples to work their way through the input buffer.
Was just looking around at doing a subset of FFT and found this:
https://electronics.stackexchange.com/questions/240594/calculating-fft-for-only-part-of-full-frequency-range
Apparently, Goertzel is FFT for just one bin.
Also Chirp Z Transform looks like it might be a fit for this:
https://www.osti.gov/servlets/purl/816417
That's why generally, a windowing function is applied before performing an FFT (and to compensate, the end of one transform overlaps the beginning of the next). That's also not perfect, but gets rid of the hard cut-off at the edges.
thanks! I'll see if I can get a handle on FIR, too.
thanks!
does anybody know about the ,,MUSIC" algorithm?
Does this discussion mean that we're closer to having a P2 equivalent of the ATG (auto-tune-guitar)?
Windowing is well known, but in the end it doesn't change anything but the signal. The point is: you can select an interval just because this interval's signal is periodical over all time. A window function brings down the signal close to the intervals ends and so forces continuation. But the price you have to pay is: you can see the signal as a carrier and the window function as a modulation, so this window function will create side bands to the carriers frequencies.
What is not known in the broad audience: the FFT is fastest when the interval's length is of 2^N, but you can also use it on signals of length 1.5 * 2^N with slightly increased runtime, the same is true for arbitrary lengths. So if you know the "real" fundamental you can select an interval of this length. Imagine you have a 1.024 second period, then 1024 samples will result in a single frequency amplitude >0. If the period is 1.1 seconds, you will see a broad spectrum. So you could iterate to find the interval that creates the spectrum of most simple complexity.
But this will not run in real time :-)
Once Fourier found a way to represent the temperature distribution on a rod by approximation of harmonic functions. And describe the cooling process by amplitudes of frequencies. There was a long way to find a linkage to e.g. group theory https://en.wikipedia.org/wiki/Fourier_transform_on_finite_groups
Fourier Transform is a universe still not fully understood.
Imagine: The FT shows you it there is a periodical behavior in a signal. Every signal is defined by (equidistantly) sampled values. The task of the FT is to find a more simple representation of this signal, we call spectrum. So we could define: a signal is non periodical, if the fourier transform is of same complexity. So a Gaussian for sure is not periodical and the FT again is a Gaussian. It's called an "Eigenfunktion" of the FT. Linear algebra allows to find many more Eigenfunktions.
We just see the tip of an ice berg!
Happy New Year!
P.S.: I do not understand the theory in the linked article, I just realize: there is more to learn.
It doesn't matter what algorithm you use. You can't fool the laws of nature. A reciprocal frequency counter (measuring the period and calculate f=1/p) works only if you have a single, pure fundamental frequency. As soon as you have harmonics, noise or a mix of several frequencies that distorts the zero crossings or trigger points of your timer, cause jitter and therefore makes the result inaccurate.
If you do an FFT you effectively serach for the highest amplitude in the frequency domain. To get enough resolution you have to sample multiple periods of the signal. As I said earlier resolution is inversely proportional to the sampling window time. To distinguish between 100 and 110Hz you have to sample at least 10 periods.
Same for FIR filters. The higher the order of the filter or the sharper the cutoff the longer the group delay has to be. This means: longer buffer and more taps and therefore more time until you get the result.
There is no way around this unless you have an oracle machine or a crystal ball chip that can look into the future.
I would start with direct mic'ing, and see if a combination of envelope sense for the trigger and ringing sense for the frequency can be good enough.
This is a very focused problem, so you could capture 40ms of waveforms, then run a best-match compare against 6N stored examples.
If you hope to fast-sense 6 bands, from 82~110Hz, that's going to need jitter/out of band disturbances under 2-3% - sounding tough, even with direct mic'ing.
How narrow do you need the detect ? eg if a frequency is exactly half way between two bins, what should happen ?
Is this a which-one single impulse frequency problem, or do you hope to have any-of-6 arrive, at any phase ?
What is needed is some kind of reporting in real time that alerts to advents in the signal. I don't know how to make this, but I can imagine what its output would look like: Messages about the signal as it changes, which would include harmonic information.
for an example of differences involved, I plotted 3 frequencies, 100, 105, 110Hz, no harmonics or noise, when all triggered at the same impulse.
The differences after 40ms are there, but not large.
great document, thanks! lots of useful associated details.
@Mickster and, a little more searching turned this up https://www.vguitarforums.com/smf/index.php?topic=21469.0
maybe there is a bit of a vacuum now in that tiny market to do it "better" (which may only mean, "more cost effective") with other unique features.
embedded in the guitar is no longer available: https://www.sweetwater.com/store/detail/PVAT200R--peavey-at-200-auto-tune-guitar-red
though the "Industry Standard Antares Autotune" is included, off guitar, in effects boxes like this now: https://www.amazon.com/dp/B0CHBFHC9X
here is an interesting quote from 2011 article when Antares we being embedded in guitar,,,and how they simplified the detection dsp with individual pickups on each string... "The hex has been around for a while, but it’s a big deal to use it in this way for guitarists since you don’t need to try to do any polyphonic pitch recognition. Literally direct note access. Also, signals add nonlinearly, so effecting each string individually has a different sound than doing emulation on the mix."
https://cdm.link/2011/05/auto-tune-for-guitars-doesnt-have-to-be-like-auto-tune-for-vocals-the-digital-guitar-future/
wasn't really what I was going for. but all very interesting.
@ngeneer
Knowing all-too-well what luddites/snobs/purists, guitarists tend to be; I saw the writing on the wall and so I snapped-up three of these guitars. Just recently, I came across another new-in-box and so now I have four.
Been through the mill for half-a-century (playing guitar) and have had all the big-name stuff but these Peavey AT-200s are keepers.
Only one of mine has the "full-pack" but I found someone who knows how to rip it and transfer it to my other three.
Sooo many guitarists regret not buying the AT-200 but the marketing was less than half-hearted. The big stores would never have one hanging on the wall because they didn't want to sell a guitar that could do the work of three or more guitars. They want the snobs to spend thousands on a piece of fancy furniture that cannot possibly compete with the AT-200's perfect intonation. Can you imagine the "WTF" looks I get from other guitarists when I switch to an open-tuning in mid song
The Headrush only has the vocal Autotune which I detest
Jam Origin polyphonic pitch recognition is pretty darned amazing. Took a few hours to get the hang of but it opens-up a whole new world. I use a puny Windows PC and the CPU doesn't seem to take much of a hit.................Would be a dream-come-true if the P2 could handle these tasks
Craig
If there was a way to do something like a Goertzel for a single frequency, plus all of its harmonics, that would be great. It would be a pitch detector, then. Twelve of those could cover the musical scale.
Twelve FFTs could do this, too. I guess I kind of asked for an FFT above.
@cgracey said:
this is kinda the approach I think will serve best in my situation at the moment.
I'm not that fast and practiced with Propeller dev to wing off an experiment or three in an evening. but, I'm more and more appreciating Spin and the development and set of delivered libraries with the PropellerTool... all much more clear what was the set of essential libraries to access the essential features of the SmartPins. Coming at Propeller development from a non-Windows world has confounded my Propeller effectiveness more than I care to think about... I've come further at being effective in the past week since I've succumbed to running a Windows machine to have access to the official supported tools. That is not to be a knock on any of the tremendous community efforts at other language/OS support for Propeller. In fact I contribute to some Patreons for they have allowed me to even experience the Propeller at all in the last year. I fully realize the essential value of the community contributions to the Propeller effort.
that was a tangent, but a developer experience I thought should get back to Parallax that maybe will help somewhere. Now I'll be more effective, and understand what I was missing coming into this community, maybe I can be a more effective contributor to help others in through what ever language/OS they're coming from.
I plan to have more focused time this weekend to do some actual code/hardware explorations and report back to this thread.
I don't think that you need too many harmonics for a string instrument. A properly tuned Guitar starts at 82 Hz and has 4 octaves. Add one for harmonics that's 60 frequencies up to 1312Hz, needing 2624 Hz sample frequency. At 200MHz clock you have 76k cycles between 2 samples.
Software Goertzel with 32*16.16 multiply needed about 125 cycles per frequency and sample, so one cog can handle all frequencies.
More than one cog can be used to start analysing in a hunting manner.
It's late, this seems to be too easy?
so, feeling my way 'round Spin2 and getting electret mic setup and trying assorted tone generation methods through a small amplified speaker on the bench... I figured I'd setup a little routine that "listened" on one core while I played assorted tones on and around the target frequency just to get a handle on methods of audio frequency detection. here is the ADC signal heard through the electret, noting all the crunchy sound of NCO tone generation on a speaker cone of dubious quality: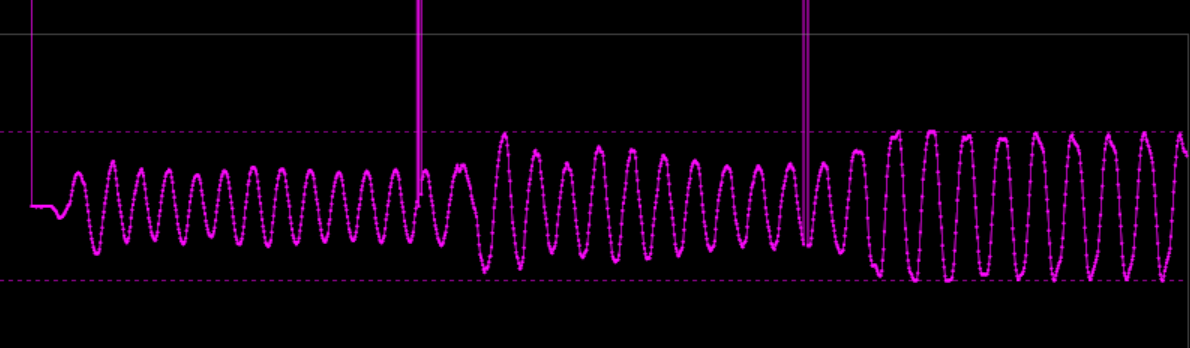
Now, it is time I go this mystical software Goertzel algorithm function