Some Code Taqoz 2.8 with inline PASM. DDS Sine Generator. ADC Sampling. Goertzel Analysis. (VGA)

Christof Eb.

Hi,
while my project will be rather specific and not of interest for too many others, perhaps some of the code routines might be helpful. I post the code as is, the project is not finished.
(My project outputs a sine signal of known frequency and amplitude to a Guitar sound effect. The output from it is sampled and analysed for amplitude and 2nd and 3rd harmonic distortion. This project has benefit using P2 instead of an other controller: Use cores without timing problems from interrupts. VGA output with enough Ram for fast graphics. Hi resolution DAC/PWM output. Programmable Gain adc input. )

There is:
1. Direct Digital Synthesis DDS Sine Generator. It generates the sine wave using cordic without a buffer and running in a separate cog. Amplitude and frequency can be changed on the fly over global variables. Versions in Forth, Hub assembler and cog LOADMOD assembler.
2. ADC sampling -one pin- into a buffer. Setting the gain factor. Sinc2 sampling, Sinc2 filter, Sinc3 filter. Hub Pasm and Forth code. (It turned out, that for my purpose Sinc2 sample mode is best suited as the other modes do not provide more than ENOB=12,4.) Forth is fast enough for 12 bit sampling.
3. Goertzel frequency analysis. This algorithm does the same as FFT but only for one frequency. So if you do only need to look for specific frequencies, this is faster and simpler. There is code in Forth and assembler. The most difficult part (for me) is the scaling. You don't want to loose precision and you have to make sure that there is no overflow, as the data adds up. In Pasm there is a signed 32bit16.16bit scaled multiply with 32bit result. The Pasm code is about 9 times faster than Forth.
4. In addition some VGA (Standard 640360, 8bit color) output is used, not pretty, but it was helpful to debug.

The picture shows best case of signal to noise analysing the DDS output directly with gain=1. Vertical axis is magnitude.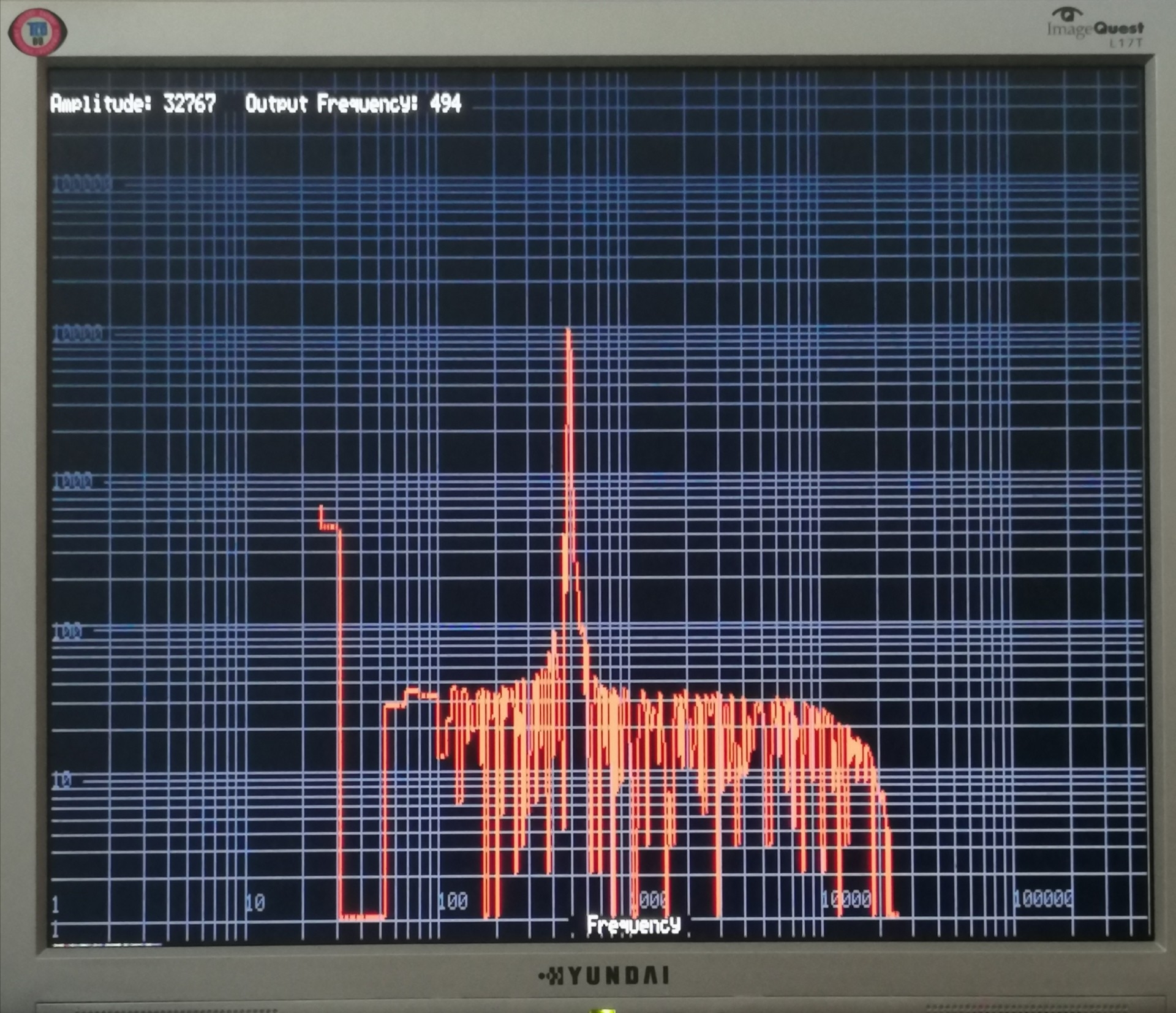

If there are ideas, how to scale the Goertzel data in a way, that mul16 can be used and still have full 12bit resolution....

Have fun, Christof

Maciek

An impressive piece of code. A pleasure to read and nicely commented. I can definitely see it getting its good use.
Thanks for sharing.

BTW, I spent a few hours yesterday playing with Tachyon just to make some simple led blinking patterns. Lots of fun resulted in less than twenty lines of not at all optimal, but working code too trivial to post anywhere

Ariba

If there are ideas, how to scale the Goertzel data in a way, that mul16 can be used and still have full 12bit resolution....

If you mean the code in goeLoopAsm then:

.l0
    mov   r2,c          '\c=16bit signed, r0=16bit signed
    muls  r2,r0
    sar   r2,#15

    sub r2,d            '\ ( q2 @ ) -
    ...

or with scas:

.l0
    scas  r0,c          '\ c=15bit signed, r0=16bit signed
    mov   r2,0-0

    sub r2,d            '\ ( q2 @ ) -
    ...

With SCAS the coefficient must be half the value, because the scale range goes from -2.0 to +2.0 (-1 LSB)

Christof Eb.

Updated the zip file in 1st post. In previous code only the real component of goertzel was calculated. Now both real and imag are taken into account. Much better.

Christof Eb.

@Ariba said:

If there are ideas, how to scale the Goertzel data in a way, that mul16 can be used and still have full 12bit resolution....

If you mean the code in goeLoopAsm then:

.l0
    mov   r2,c          '\c=16bit signed, r0=16bit signed
    muls  r2,r0
    sar   r2,#15

    sub r2,d            '\ ( q2 @ ) -
    ...

or with scas:

.l0
    scas  r0,c          '\ c=15bit signed, r0=16bit signed
    mov   r2,0-0

    sub r2,d            '\ ( q2 @ ) -
    ...

With SCAS the coefficient must be half the value, because the scale range goes from -2.0 to +2.0 (-1 LSB)

Thank you, Ariba!
The problem is, that the value in c is growing with the number of samples. So for c at the moment more than 16 bits are needed. At the end in the Forth code the result is divided by the buffer length. It is this code in micropython (from: https://forum.micropython.org/viewtopic.php?t=7290 last post ):

def goertzel(target_freq, sampling_freq, data):
    '''
    When searching for a specific signal tone the Goertzel algorithm can be more efficient than fft.
    This routine returns magnitude of a single fft bin, which contains the target frequency.
    Ideally, the sampling frequency should be an exact multiple of the target frequency (see fft window functions)
    The bin width is sampling_freq / len(data).
    E.g. 200 samples at 10kHz sampling freq gives 50Hz bin width. The bins would be:
    Bin 0:    -25 Hz  to    25 Hz  (centre:    0 Hz)
    Bin 1:     25 Hz  to    75 Hz  (centre:   50 Hz)
    Bin 2:     75 Hz  to   125 Hz  (centre:  100 Hz)
    ...etc
    So, make sure your target frequency is a bin centre frequency and sampling_freq = n * target_freq
    where n is any integer.
    '''

    #You can pre-calculate much of this stuff to save time if calling multiple times
    numSamples = len(data)
    scalingFactor = numSamples / 2.0
    k = round(numSamples * target_freq / sampling_freq)
    omega = 2.0 * math.pi * k / numSamples
    sin_omega = math.sin(omega)
    cos_omega = math.cos(omega)
    coeff = 2.0 * cos_omega

    q0=q1=q2=0

    #The following loop calcs can be done sample-by-sample to spread CPU load if required, much like a filter.
    for i in range(numSamples):
        q0 = coeff * q1 - q2 + data[i]
        q2 = q1
        q1 = q0

    real = (q1 - q2 * cos_omega) / scalingFactor
    imag = (q2 * sin_omega) / scalingFactor

    magnitude = math.sqrt(real*real + imag*imag)
    return magnitude