Combinational key matrix 4 I/O=10 keys, 8 I/O=36 keys
 Peter Jakacki
Posts: 10,193
Peter Jakacki
Posts: 10,193
We are used to simple key inputs and when we have a lot of keys we used an XY matrix. If we only have 4 I/O that gives us 4 keys or with a 2x2 matrix that still only gives us 4 keys with no advantage. But what if 4 keys were simple direct non-scanning inputs so that any one can pull down an I/O line. That's 4 of course but now we place keys across the combinations of the 4 inputs. Then by checking first that no direct button is pressed (all highs) we then pull one I/O down and check the other 3 for a low indicating a combo key is pressed?
How many other keys can we add? The answer is 6 so with the 4 in total we can have 10 keys. With 5 I/O we can have 15, with 6 we can have 21, and the scan logic is very simple.
Any of the commoned keys (directly grounded) can directly affect the I/O but the combo keys need to be scanned.
For 4 I/O labeled A B C D we get the combinations: A B C D AB AC AD BC BD CD
Even if you didn't have a ground and only 4 physical wires you could still read 6 keys.
This reminded me of Charlieplexing LEDs and so I just did a quick search for doing the same with switches but from the little I could find they seem to be using diodes.
Anyway I don't know what to call it, maybe "ultraplex" but this method is ultra-simple and your typical 4x4 matrix normally yields 16 keys but those same 8 I/O will handle 36 keys this way.
The basic formula is n*n/2+n/2 so 8*4+4 =36 or n^2/2+n/2 or just add up the sequence like this 8+7+6+5+4+3+2+1 = 36
136 keys need 16 I/O.
I will build up a circuit later and write a q&d key scanner but here is what the circuit looks like. (assume pull-ups)
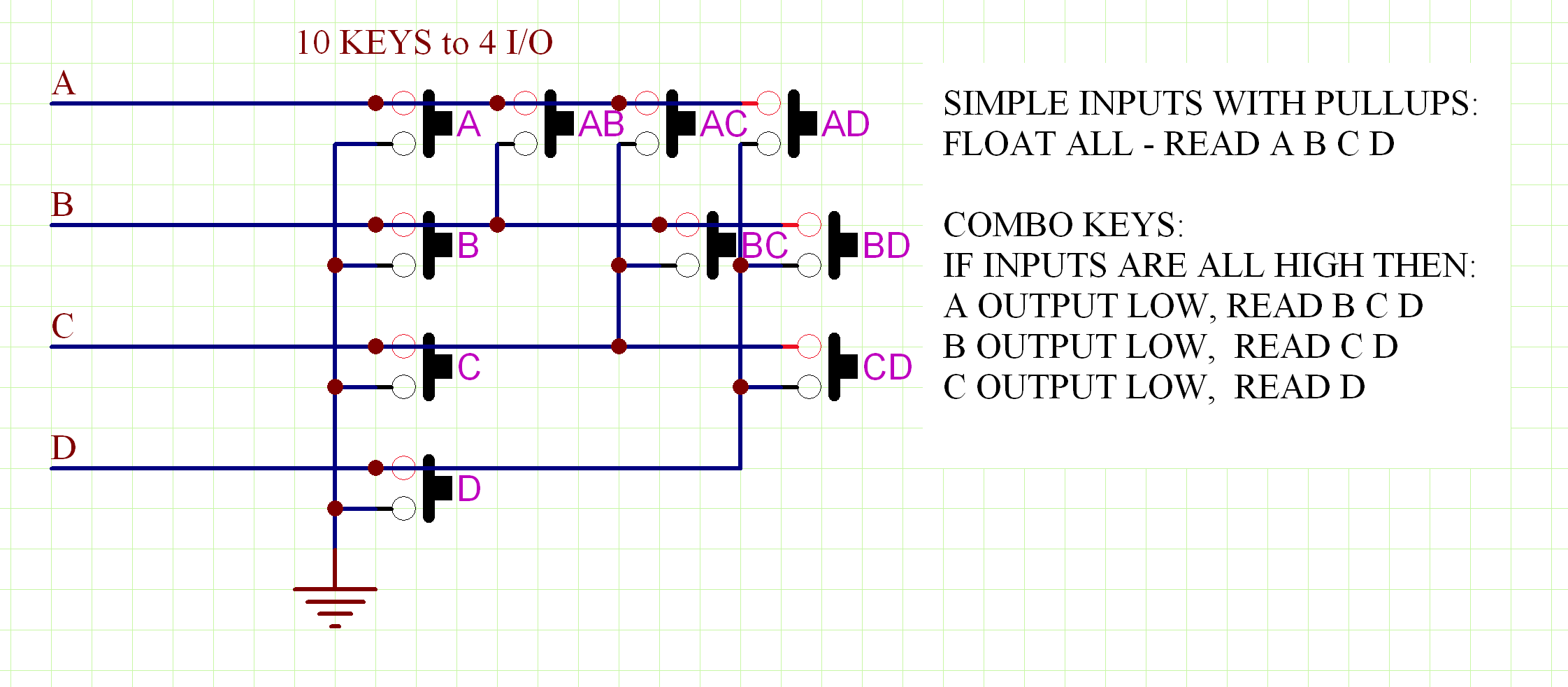
How many other keys can we add? The answer is 6 so with the 4 in total we can have 10 keys. With 5 I/O we can have 15, with 6 we can have 21, and the scan logic is very simple.
Any of the commoned keys (directly grounded) can directly affect the I/O but the combo keys need to be scanned.
For 4 I/O labeled A B C D we get the combinations: A B C D AB AC AD BC BD CD
Even if you didn't have a ground and only 4 physical wires you could still read 6 keys.
This reminded me of Charlieplexing LEDs and so I just did a quick search for doing the same with switches but from the little I could find they seem to be using diodes.
Anyway I don't know what to call it, maybe "ultraplex" but this method is ultra-simple and your typical 4x4 matrix normally yields 16 keys but those same 8 I/O will handle 36 keys this way.
The basic formula is n*n/2+n/2 so 8*4+4 =36 or n^2/2+n/2 or just add up the sequence like this 8+7+6+5+4+3+2+1 = 36
136 keys need 16 I/O.
I will build up a circuit later and write a q&d key scanner but here is what the circuit looks like. (assume pull-ups)



Comments
-Phil
Not really worried about multiple key presses although some obviously would be valid. This is mainly for those times when we have 4 I/0 for example and more than 4 keys to handle. Invalid key combinations are invalid combinations, no problems. These small keypads and button inputs aren't being handled by a 2 handed touch typist but are normally by means of the George Jetson index finger.
I thought I had done something similar back in the 80's to save using diodes. I just checked and no. I freed up enough pins on the micro to read them directly.
While looking I found my circuit diagram done with LisaDraw back in '83
btw, a conventional 4x4 keypad matrix can only read 16 keys and up to 4 keys can be pressed at the same time as long as they don't conflict. With ultraplexing those 8 I/O can read up to 36 keys and the 8 direct keys can be operated at the same time, as well as other combinations.
Can help poke at your math... it looks like your formula breaks down to n! (n factorial).
Factorial of 4 is 24 = 4x3x2x1 whereas this is 4+3+2+1 = 10
sum not product - so maybe a sigmaplex
It's possible to get the occasional wrong scan code, I think, when the user presses a key just after the program has read the "simple keys" and decided that it needs to scan. But this is probably easy to cater for by making the key debounce testing (which is always required for switch contacts) look for consecutive scans returning the same result before registering the initial 'key down' event.
Even simple button presses need some kind of debounce, and this would be no different. Read a code, wait, reread and verify. Direct keys that are grounded don't need scanning and work just like simple push-buttons switches would anyway. But when all is quiet then the indirect keys can be scanned and debounced too.
Hey, I thought of that too seeing Charlie somebody got perplexed about what to call his stuff. If Ultraplex or sigmaplex falls through, then why not have a PeterPlexed keypad!
Yes - but for the fastest response with a normal matrix keyboard, you don't necessarily have to debounce the 'contact made' events - only the 'contact released' ones. With your improved system, you need to 'debounce' both edges of the signals - but that's a small price to pay for being able to scan lots of extra keys with the same number of I/O.
As I said, you always need a debounce routine for mechanical contacts. Some standard matrix keyboard scanning routines probably already debounce the 'make' as well as 'break' edges, and I agree that adding such an extra check, if needed, is trivial to do.
Peterplexed keypad +1
BTW, I used the A/D technique on vending machines decades ago where I wanted to reduce the wiring harness to the front door and used resistors and also diodes. Later I even designed a long sensor strip pcb with large copper sensor pads that could detect cards being vended just by the variation in capacitance and having one section as a reference. No A/D required there, it just needed a comparator and a pulse and some timing. I could tell how far in or out the card was unlike the troublesome microswitches or lever trigger opto-switches that it replaced. The sensor strip had its own tiny AVR just for the job.
If you have a 12-bit resolution A/D, you could in theory read up to 4095 keys, but probably 500 keys would be enough for most! And the contact resistance of the key doesn't matter much, because it's just connecting a potential divider (the resistor pair) to the A/D input - any contact resistance is likely negligible compared to the input impedance of the A/D.
If you chose the values of the resistors carefully, you'd also be able to decode two (possibly more) keys pressed at the same time!
A resistor ladder, rather than a pair for each key, would cut down the number of resistors to the same as the number of keys (plus one or two for the final rungs of the ladder to VCC and/or GND).
This will easy a lot any debouncing logic, mostly avoiding timeout-waiting-related dead times.
Also, by properlly adjusting filtering values, to ensure minimum bit-timings, I believe (though I'm not sure yet) you could even leverage from the use of some Pulse Position Modulation protocol, to ease the identification of wich pins are interconnected, if any.
Sure, that would tottaly dismiss the use of any direct-connection to GND, but would otherwise enable the possibility of using an asynchronous serial protocol, where each received symbol would reflect the interconnection paths.
Must put it onto some timing charts, just to be sure it's feasible, but, if it works, would immediatelly show how far we can reach with P2 and its smart pins.
This is a console test and the result when I press the buttons from left to right and back again. The test waits for a valid key then emits that to the console then waits for a release and continues until a console key is pressed
The code (194 bytes). It sets up the pins as 1K5 pullups with an active sink to allow it to drive it low. The keys can be on any port and I used a method to read all pins in one operation so it had to know which port it was on, but this could be done differently. If no direct grounded keys are found, it will then scan for the bridged keys. Any key found is converted to a code which is then translated to ascii in a lookup table (an ascii string actually).
btw - I made a mistake initially with not writing pullup modes to the pins and found that I can draw 63.5ma from a shorted pin
TAQOZ pub *PPKEYS* PRINT" PeterPlexed keypad demonstration 200818.0000 " ; --- constants #P16 := KEYPAD --- first I/O line of keypad 4 := KEYS --- number of I/O lines for direct keys KEYS |< 1- := KEYM --- internal mask KEYPAD 5 >> INA + := KEYP --- internal port to use pub READ_PPK ( --- inputs ) --- set all I/O as pullup drive low set KEYPAD KEYS PINS 1K5 PULLUP CMOS SINK 0 WRFNC H --- read port A or B and extract the 4 bits KEYP COG@ KEYPAD >> KEYM XOR >N ; --- scan for bridged keys that may be pressed pub SCAN_PPK ( -- code ) --- Q&D loop through combinations and return with a code if found --- 1st pin range-1 KEYPAD KEYS 1- --- pin low then scan remainder (25 COG@ to read the loop limit or final i/o line) ADO I LOW $25 COG@ 1+ I 1+ --- pin low? yes, create a code with offset and quit loops or keep looping DO I PIN@ 0= IF J KEYM AND 2 << I KEYM AND + KEYS + UNLOOP UNLOOP EXIT THEN LOOP LOOP 0 ; pub PPK@ ( -- code ) --- read direct and encode else scan keys READ_PPK ?DUP IF >| 1+ ELSE SCAN_PPK THEN --- translate 4-bit code to ascii DUP IF " ?0123456??78???9" + C@ THEN ; END { --- interactive testing will print the code - ascend and descend keypad BEGIN PPK@ ?DUP IF EMIT BEGIN PPK@ 0= UNTIL THEN 20 ms KEY UNTIL --- 0123456789876543210 --- timing how long it takes to scan all with no result TAQOZ# LAP PPK@ LAP .LAP --- 6,049 cycles= 30,245ns @200MHz ok }So a triangular number then.
X = (n * (n+1)) / 2