Optimum COVID-19 Testing Pool Size vs. Positivity
 Phil Pilgrim (PhiPi)
Posts: 23,514
Phil Pilgrim (PhiPi)
Posts: 23,514
The news lately has suggested that COVID-19 tests could be done more efficiently by combining, say, 25 samples into one batch and testing the batch as a whole. Then, if the batch tests positive, go back and retest individuals within the batch. This has the potential of reducing the total number of tests required. (BTW, it's not clear from the reports I've read whether two samples are taken from each individual, so they don't need to be called back, or whether those individuals in a positive pool need to return for another test.)
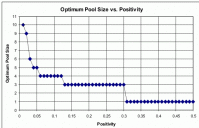
This got me to wondering, given a known percentage of expected positive tests (the "positivity" number), what the optimum pool size would be to minimize the total number of tests required in a given population. So I wrote a program in Perl that does a Monte Carlo simulation of the testing regimen for a population of 100,000 individuals, for pool sizes ranging from 1 to 50, and positivities from 0.01 to 0.50. Here's the program:
The optimum pool sizes were pretty low, starting at 10 for a positivity of 1% and dropping rapidly as the positivity increased. Above a positivity of 30%, there was no advantage to using pooling, as the graphs below demonstrate:


I was hoping to send my results to the CDC or NIH, but I was scooped! The following paper appeared in JAMA last month:
https://jamanetwork.com/journals/jamanetworkopen/fullarticle/2767513
At least it was nice to see that their results agreed with my own!
-Phil
P.S. If anyone objects to my posting this here, due to its lack of any relation to Parallax or its products, I might be happy to rewrite the Perl program in Spin.
This got me to wondering, given a known percentage of expected positive tests (the "positivity" number), what the optimum pool size would be to minimize the total number of tests required in a given population. So I wrote a program in Perl that does a Monte Carlo simulation of the testing regimen for a population of 100,000 individuals, for pool sizes ranging from 1 to 50, and positivities from 0.01 to 0.50. Here's the program:
use strict;
$|=1;
my $population = 100000;
foreach my $i (1 .. 50) {
my $positivity = $i / 100;
my $min_tests = 1e38;
my $best_pool;
foreach my $pool_size (1 .. 50) {
my $ntests = do_tests(100000, $pool_size, $positivity);
if ($ntests < $min_tests) {
$min_tests = $ntests;
$best_pool = $pool_size;
}
}
print "$positivity $best_pool $min_tests\n";
}
sub do_tests {
my ($population, $pool_size, $positivity) = @_;
my $ntests = 0;
foreach (0 .. $population / $pool_size - 1) {
$ntests++;
foreach my $test (0 .. $pool_size - 1) {
if (rand(1) < $positivity) {
$ntests += $pool_size unless $pool_size == 1;
last
}
}
}
return $ntests
}
The optimum pool sizes were pretty low, starting at 10 for a positivity of 1% and dropping rapidly as the positivity increased. Above a positivity of 30%, there was no advantage to using pooling, as the graphs below demonstrate:


I was hoping to send my results to the CDC or NIH, but I was scooped! The following paper appeared in JAMA last month:
https://jamanetwork.com/journals/jamanetworkopen/fullarticle/2767513
At least it was nice to see that their results agreed with my own!
-Phil
P.S. If anyone objects to my posting this here, due to its lack of any relation to Parallax or its products, I might be happy to rewrite the Perl program in Spin.



Comments
-Phil
Was that a gauntlet laid splendidly and spinningly on oneself, Phil?
-Phil
By comparing the cases v deaths, the ratios don’t match very well. It seems the case numbers reported are either so far under the actual cases, or the medical facilities are terrible in some countries.
Pubs reopened on the 4th and so now I can enjoy a proper sit-down meal.
Place is busy, no social distancing...people in groups and rowdy as they used to be.
But nobody is trying to topple a President here. Just sayin. Prolly get deleted anyway.
And Phipi, tip-top work as always. Will YOU please consider a PotUS nomination?
With the limit-of-five in mind, I reran the simulation and got these results:
-Phil
Of course the dilution can be offset by designated no-shows.
https://www.nytimes.com/2020/08/21/health/fast-coronavirus-testing-israel.html
By using a combinatoric method akin to error-correcting codes, the scientists claim ability to test 384 individuals using only 48 tests, with no repeat testing required for positive samples. They do this by distributing each person's sample among several pools in such a way that a spectrum of positive tests will reveal the positive individual(s). There are some caveats, though, namely an upper limit on overall positivity for the method to work, and dilution due to the rather large pool sizes involved. The latter is concerning in light of other research noted in my post above.
-Phil