Weekend Puzzle
 Phil Pilgrim (PhiPi)
Posts: 23,514
Phil Pilgrim (PhiPi)
Posts: 23,514
I'm designing a marble puzzle to give as a gift. It involves a tight circle of marbles around a larger disk. I know the radius r of the marbles, and I know that I want n marbles around the disk. What radius R do I need to make the disk, so that n marbles just fit around it? Here's a illustration:
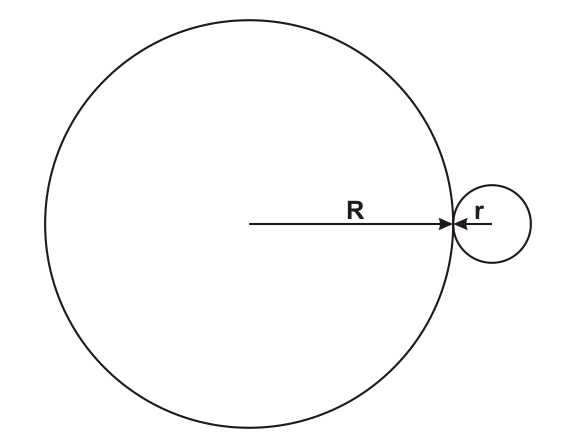
'Turns out to be an interesting geometry problem. See if you can provide a formula for R in terms of n and r.
Hint: Test your formula when n = 6. In this case R must equal r.
-Phil

'Turns out to be an interesting geometry problem. See if you can provide a formula for R in terms of n and r.
Hint: Test your formula when n = 6. In this case R must equal r.
-Phil


Comments
The solution lies in correlating the center points.
4 marbles grouped together make a predictable square with their center points.
The diameter for the inner circle is the diagonal of the square - 2 times the radius (or simply the diameter) of a marble.
Thus the formula for the can be extracted as the (diagonal of an n-gon with even sides all the length of 1 marble diameter) minus the diameter of 1 marble.
:-)
2r = 2*(r+R)*sin(180/n)
rearranging for R, I get
R = (r / sin(180/n)) - r
or, for those who prefer something easier to read
R = r(csc(π/n)-1)
-Phil
There is a right angled triangle, ABC, formed by the center of the large circle "A", the center of a small circle "B" and the point at which the small circles touch "C"
The angle BAC = PI/n (Because we have a n sided polygon formed by the centers of the small circles)
The distance BC = r
The distance BA = R + r
By trig:
sin(BAC) = sin(PI/n) = r / R + r
Rearranging for R:
R = r / sin(PI/n) - r
Q.E.D.
-Phil
-Phil
If you need a Sunday puzzle we can step this up a bit.
A special case of your problem is when n = 4. Let's make r = 1/4. Then we have 4 circles packed into in a square of side 1. The unit square. With our solution we can obtain the radius of the circle that fits in the middle of the square and touches our other circles.
How about we lift that into 3 dimensions? Then we have 8 spheres packed into a unit cube. What is the diameter of the sphere that just fits there in the middle touching each of the 8 other spheres?
Let's keep going. We can back sixteen 4-spheres of radius 1/4 into a four dimensional cube (hypercube) of side 1. What is the diameter of the 4-sphere that fits in the space in the middle?
What about 5, 6, 7... dimensions?
At what number of dimensions does the sphere in the middle get bigger than the box it is packed into?
That last result is a bit of a mind bending surprise.
"It is left as an exercise to the reader to determine the necessary formulae..."
"It shall be tacitly assumed that the reader is familiar with the requisite geometry..."
The little seedling grew and grew, until one day it exclaimed, "Ge...om-e-try!"
"It can be seen that.."
At that point I know I'm lost.
Thanks for the puzzle! I've been on a puzzle-solving kick lately, so this was perfect timing.
(For those looking for a holiday themed coding puzzle, check out http://adventofcode.com.)
Now a days I can spend hours soaking up these guys:
https://www.youtube.com/user/blackpenredpen/featured
https://www.youtube.com/channel/UC1_uAIS3r8Vu6JjXWvastJg
https://www.youtube.com/user/numberphile
https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw
They take care to step through every detail and seem to be having a lot of fun doing it.
There is a "spoiler" button "?" shortcut when adding a post to the thread
Of course, this isn't strictly correct, as we are letting the diameter of the marble be the 1/n of the circumference but it is in reality the Chord at the circumference.
In order to get accuracy, we need to employ SIN/COS/TAN theory, and the chord of the circle.
If we have 'n' marbles at a radius of (R+r), the angle made by joining the two adjacent centres of the marbles (call these 'M1' & 'M2') to the centre of the circle (call this 'C') will be 360degrees/n. We know the dimensions C.M1=C.M2=R+r and we know that angle M1.C.M2=360/n degrees.
The chord M1.M2 formed on the circle with radius (R+r) will have a length of 2*r because the two marbles will touch at this point, and each marble is radius r. The mid-point (the point at which the marbles touch) we will call Mx, and M1.Mx=Mx.M2=r. The line C.Mx will be at right angles to the chord M1.Mx.M2.
Now we have two triangles formed by M1.C.Mx and Mx.C.M2 where angle M1.C.Mx=Mx.C.M2=360/n/2 degrees = 180/n degrees, and a right angle formed at M1.Mx.C and Mx.M2.C.
Therefore our small triangle M1.C.Mx has M1.C=(R+r), M1.Mx=r, M1.Mx.C=90degrees, and M1.C.Mx=180/n degrees.
Therefore,
SIN(180/n)=r / (R+r) = opposite/hypotenuse
Solving for R ...
(R+r)=r/SIN(180/n)
R = r*(1/SIN(180/n) - 1)
So for n=6 ...
R = r*(1/SIN(30) -1)
R ~= r*(1.012 -1)
R ~= r * 0.012
BTW Had to give this some serious thought. Just realised I am quite rusty, or is it just a "senior moment"?
So the cheap-@$$ Chinese checkers marbles I bought range in size from <0.54" to >0.56". Some of them aren't even round. So I've had to caliper all of them and sort them into 0.005"-increment bins. Hopefully, I'll have enough of each color in a small cluster of bins to pull this off. I think I can keep the diameters within 0.02" of each other, but that's pretty lax. Otherwise, I'll have to buy more marbles and go through the same exercise until I've got enough of the same size.
-Phil
Seems I used a SIN calculator with radians instead of degrees. Highly embarrassed
In the old days, I would have known sin(30degrees)=0.5=cos(60degrees) without tables/calculator.
Try a Chinese Checkers game at Target. You can check it in the Starbucks and return it in perfect condition if they are no good.
Wait what?
A radian is an a priori concept, when did we figure them out?
I guess radians have always been a part of my world.
I can't determine which idea about measuring angles came first, radians or degrees.
But the radian like idea seems to date back to al-Kashi in 1400 or so. Although the word "radian" comes four hundred years later.
To my mind it goes like this:
1) With a ruler you can draw a straight line.
2) With a pair of compasses you can mark off distances along that line. Call each step 1.
3) To break out into two dimensions you can easily draw a circle with your compasses. Radius 1.
4) But then you see that you can easily construct an equilateral triangle with your compasses. Each side of length 1.
5) Then you see that you can continue that construction and make a hexagon. Each edge of length 1.
6) But that hexagon fits inside a circle of radius 1.
7) Conclusion is that the circumference of a circle is a bit more than 6.
8 ) So now it's obvious that to turn a full circle you have to sweep out a distance of a bit more than 6 along that circumference.
9) Clearly a full turn is 6 and a bit or 6.something as we might say to day.
10) So obviously fractions of a turn should be fractions of 6.something. For example turning around to face the opposite direction would be an angle of 3.something.
The point of all this is that the fundamental ratio, the circle constant, is 6.something. Call it Tau. Today we know it more accurately as 6.28318531.....
Unfortunately, somewhere along the line somebody messed this simple logic up and defined the circle constant as π=3.141592.... Only half what it should be. That is to say they decided on the circle constant being circumference/diameter rather than radius/diameter. That latter being more natural when you start with a ruler and compass as the early mathematicians did.
Which has confused students ever since.
Most of my algebra students are either under 10 or over 24 so I really have to spell it out.
I teach pi by inscribing a circle within a box on a large sheet of graph paper, then dividing the box into 4 even quadrants, and direct the student to focus on a single quadrant.
From there we measure the length of one quadrant leg from the center out, and we note that it's also the radius of the circle.
Then I have the student count all the boxes in the circle quadrant and square the radius to get all the boxes in the quadrant.
Based on that I have them predict how many are in both the entire circle and in the entire square.
When the divide the two whole to quadrant ratios they get 4 and 3.1ish.
This helps them get a handle on about what pi is and how it applies to the area of a circle.
Then we examine 2 quadrants together. Noting the distance across both quadrants is 2 times the radius, and call it the diameter. We start at the diameter perigee and trace the outer edge of both quadrants and note that it is 2 times the diameter and that the whole square will be 4 times the diameter.
Then we roll a ruler along the semi-circle and divide that value by pi. This takes them back to the radius and from there we get multiply by 2 to get the whole circle and the formula for the circumference.
This is the time that I teach radians as well. We talk about words with roots common to radius: radial and radian. Most students know of the word radial and they usually go straight to tires and the light bulb turns on. Then we look back at the math for the circumference and realize that it takes 2 pi radians for the circumference and note that 'r' is just a symbol and can be named whatever we like to understand the problem. So we say if r is straight it's a radius and if it's curved it's a radial radian, because alliteration is fun.
I had a great geometry teacher. She only taught proofs and application, never axiom. Her tests were the same and she never marked off for getting a name wrong if the math was otherwise correct. Most of my lessons are from her teachings and what I read about the ancient Greeks' lessons.
https://tauday.com/tau-manifesto
This all started out as something of a joke. But over the years since then I have become more convinced of the sense in it.
Specifically, the diameter of a circle is not the fundamental concept. The radius is.
Like I said, when you have a pair of compasses you set the legs apart, the radius, spin it around, boom you have a circle. The diameter is something you have constructed from the radius. As is the circumference and the area. Clearly the circle constant should be based on the most fundamental thing, the radius.
How is that possible?
All proofs are founded on axioms. Think Euclid and onwards.
Of course you are free to start from different axioms if you like, for fun. Hence non-eclidian geometry and such.
If we used tau instead of Pi, then the area of a circle would be 1/2*tau*r^2. I would rather use pi*r^2 and circumference 2*pi*r = pi*d. As such, I disagree with the tau proponents - I am in the PI camp.
BTW I don't recall any talk about radians at school (I did the highest level maths which was 11 x 40 min periods of 36 (plus 4 lunch periods) per week. Did the same for Science. In retrospect, I must have been stupid
I cannot recall when I became aware of radians. We used slide rules as portable calculators were just on the horizon when I finished my electronics course. I think it might have been the spreadsheet that first introduced me to radians.
So am I -- obviously. The phi camp, too.
-Phil
I've always thought the diameter was just another construct of the radius but never so far as to correct pi. It does a heck of a job on trig as ratios of the circle. I have an issue with it replacing pi when it could do a better job augmenting pi. e^itau = 1 is a solid argument, but e^ipi = -1 is also a sold argument for pi. I've never understood peoples' fear of -1 and imaginary numbers. They aren't fake, they just aren't part of the Real Number Set. Unfortunately as they are 90 degrees off reality, they are technically imaginary but they are no less valid. The current flow across a capacitor is imaginary yet a capacitor is defined by its ability to store that current. I like them both.
Interestingly, pi and tau could form a symbiotic proof based on his analysis of Euler's Theorem as an empirical case by observing any point and its polar opposite starting with e^i0 and going anywhere from there. Which pairs deliciously with his use of the yin-yang. In fact there is historic precedent for the mathematical importance of polar opposites. The most profound being 0. The concept that is nothing but arguably equally as important as something ad represented as something containing nothing. Peace is about balance of polar opposites which is embodied in the yin-yang. Perhaps he should have researched the spiritual importance of tao before using it in such an ironic way.
In his circular area proof he just proof that tau does work well in calculus but it's a circular proof in that the justification requires the contrary proof to begin with. To me this justifies the use of both.
He even says more than once, "You're going to be tempted . . . " Well, since all math is just our symbolic interpretation of a concept that is without time why not simplify and use both as they both have a solid meaning.
Followed up by, "you sometimes have to work really hard to figure out what's going on."
Why? If you accept both you cut your proof workload in half, literally and figuratively.
His work is fantastic, correct and insightful, but his conclusion that one is superior to the other is a completely false and unproven here.
The area of a circle is pi r^2, tau = 2 pi, and the circumference is tau r. This is not complicated.
My geometry teacher only ever built on previous concepts. There is/was the assumption that the student had a working knowledge of algebra I concepts. Either absolutely or empirically every concept was proven to us and the subsequent quiz was always on the proof and one or more applications of it.
The proof of the volume of a sphere as the intersection of cylinders was just fascinating.
I don't see anyone bothering to memorize Tau to 67,890 digits.
Hardly my fault they wasted their time memorizing the wrong number
Now, if they had memorized it in binary they would have both. Just have to shift up by one place.
-Phil
Personally I think the Real numbers are misnamed as well. That includes root 2 and PI and all that. Which you can't even write down. You can't even count them all! You can't even count how many you have between 0 and 1. How imaginary can a thing be?