Haversine - GPS Utilities

DPdiesel

Hello All,

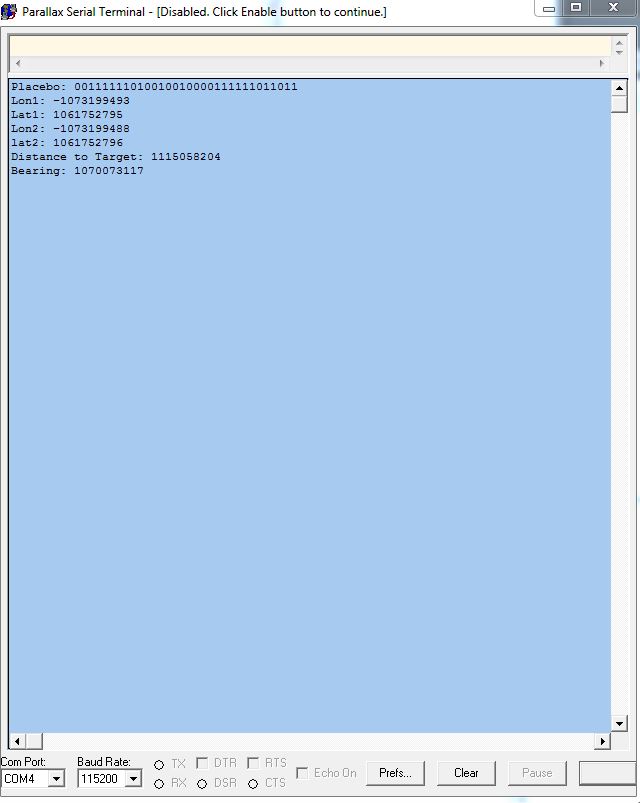
I am struggling to effectively implement the haversine formula to determine the azimuth and distance between to points with lattitude and longitude. I found an object labeled GPSutilities that looks like it does what I want however when I test the logic and get a result, I cant make heads or tails of the result. I found a few errors in the objects that once corrected I was able to get data out, but again, I have no idea what I am getting. The data does not return what I expect. For instance when I use GPS coords less than a mile apart I am getting a very large value for distance 1.07E9. I speculate it is the way I am handling the data, from Rads to FP to decimal something is being lost in translation. Attached is the code and picture of the output via PST.

I would appreciate any insight, objects of another direction, corrections to the code. Anything at this point.

I am pretty green to the propeller. Be gentle

Phil Pilgrim (PhiPi)

Are you sure you even need to use the spherical formula (the one with haversines)? For short distances, a simple planar approximation will probably be good enough for most purposes. Here's what I use:

ΔY (meters) = (Latitude₁ - Latitude₂) * 111319
ΔX (meters) = (Longitude₁ - Longitude₂) * 111319 * cos(Latitude₁)
Distance = sqrt(ΔX² + ΔY²)

BTW, if you maintain your coordinates in millionths of a degree, you can avoid floating-point math and still have reasonable accuracy.

-Phil

DPdiesel

PhiPi,

No, I am not sure. I use this across a distance of < 30miles. I am not sure how much accuracy I could expect one way or the other but I will certainly give your straightforward equation a test run.

For elevation I am using: ATan (Height/distance) which I believe should work but negates curvature as your equations do. Ideally I would like to learn how to arrive at this using spherical as well but that may be a task for later. I digress.

Based on my previous post. Any thoughts on what the data I am looking at is telling me? I have tried to back calculate it every way I can thing of.




When you say use to maintain my coords in millionths of degrees? Do I multiply the decimal out and the divide later? I am not tracking

WBA Consulting

I don't recall all of the details to remember if these threads will help out, but anyhow, the code does calculate distances between two points correctly:

http://forums.parallax.com/showthread.php/155282

http://forums.parallax.com/showthread.php/133806

SRLM

It looks pretty good to me. Maybe try setting the floating point values directly instead of using the `convert2Radians` function?

Phil Pilgrim (PhiPi)

DPdiesel wrote:

When you say use to maintain my coords in millionths of degrees? Do I multiply the decimal out and the divide later?

Yes, multiply the decimal degrees by 1_000_000. Do your computations first, then divide by 1_000_000 to get meters or by 1_000 to get mm. One huge caveat, though: at your distances (> 19 km) you will get 32-bit integer overflow. The stuff I do involves distance of less than a kilometer, so that's not a problem.

-Phil

max72

I posted this object:
http://forums.parallax.com/showthread.php/128884-integer-only-GPS-navigation-object

cross track is not working well, but everything else works.
I used an integer only approach, using nautical miles multiples, cordic and conversion to meters.
It's spin only.
It parses the gps coordinates and converts them to integer.

At this distance earth is reasonably flat... if you check the difference with haversine it's minimal, unless you are navigating around poles...

Massimo

msrobots

Phil Pilgrim (PhiPi) wrote: »

Yes, multiply the decimal degrees by 1_000_000. Do your computations first, then divide by 1_000_000 to get meters or by 1_000 to get mm. One huge caveat, though: at your distances (> 19 km) you will get 32-bit integer overflow. The stuff I do involves distance of less than a kilometer, so that's not a problem.

-Phil

Well going down to 500_000 on the multiply/divide with less resolution should solve the overflow problem, I guess. Integer is always faster then float.

@DPdiesel

As for the difference of 'Havesine' to the 'flat earth model' I am quite sure that even in a distance oft 32 miles the natural unevenness of the ground is way greater then the mathematical difference between both models.

And you also have to accept that GPS is not as accurate as some people think. Even stationary the position may move around in a area of 50 by 50 foot.

So calculating distance in meters is already a challenge, forget even to think about millimeters. The data you get from GPS will not deliver this. If you can get a accuracy of 10 meters you are quite good already.

Therefore you will not need floating point. Use Integers and scale them up as less as you need for your minimum requirement resolution. To leave enough space in the 32 bit number for computation.

just my 2 cents.

Mike

DPdiesel

I have worked on some of the approaches suggested. My recent approach uses: Float32Full
current_lat := 45.0
current_lon := 122.0
latRads1 := f32.radians(current_lat)
lonRads1 := f32.radians(current_lon)

This returns the value in PST of:
Latrads1 = 1061752795
Longrads1= 1074284155

I am at a loss here of what these values represent. I am using the pst.dec command to display the floating point. does the value need to be truncated or converter to integer or what?

Phil Pilgrim (PhiPi)

DPdiesel wrote:

I am using the pst.dec command to display the floating point.

That's your problem. pst.dec is only for integers. Use the library object FloatString.spin to convert floats to a string that you can print.

-Phil

DPdiesel

Phil Pilgrim (PhiPi) wrote: »

That's your problem. pst.dec is only for integers. Use the library object FloatString.spin to convert floats to a string that you can print.

-Phil

Thanks Phil!!! The values displayed now look reasonable...imagine that.

moving on....I am going to throw up my next question here and avoid another thread. I am having what I think is a roll over issues. When my bearing value rolls from 360 to 0 or vice versa I am getting a math overflow??. (6.805647e+38) I am using a prewritten object that I think I understand and it appears to handle this situation but I don't believe that it is. Let me know if I should post the whole code, I can do. It is working perfectly until the bearing changes across 360.

pub CalcBearing(lat1,lon1,lat2,lon2,distance) : bearing | t1,t2,t3,t4,t5
'' lat1,lon1,lat2,lon2,distance are floating point variables in radians
'' Returns bearing in floating point radians

t1 := fp.fsub(fp.sin(Lat2) , fp.fmul(fp.sin(Lat1) , fp.cos(distance)))

t2 := fp.fmul(fp.cos(Lat1) , fp.sin(distance))

t3 := fp.fdiv(t1,t2)

t4 := fp.fadd(fp.atan(fp.fdiv(fp.fneg(t3),fp.fsqr(fp.fadd(fp.fmul(fp.fneg(t3) , t3) , 1.0))) ) , fp.fmul(2.0 , fp.atan(1.0)))


if (fp.fcmp(fp.sin(fp.fsub(Lon2 , Lon1)),0.0) < 0)
t5 := t4
else
t5 := fp.fsub(c2pi , t4)


bearing := fp.degrees(t5)

return bearing