Key/Lock Puzzle

Phil Pilgrim (PhiPi) · 2013-12-03 15:10

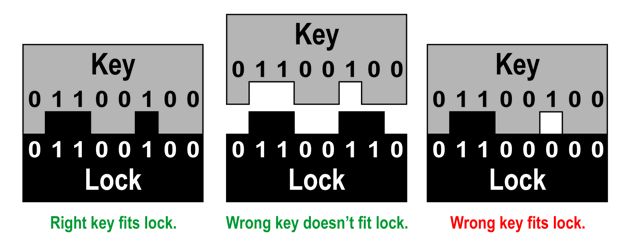
I'm working on a mechanical puzzle that requires 256 "keys" and 256 "locks." Each key must fit one and only one lock. Unlike a traditional tumbler, though, if a key can be pushed into the lock, it's deemed to fit. The keys are coded in binary, as shown below:

attachment.php?attachmentid=105360&d=1386111878

attachment.php?attachmentid=105360&d=1386111878

As is obvious from the far-right image, not all binary combinations of keys and locks are suitable, since we don't want a wrong key to "fit." So the puzzle is this: how many bit positions, and what binary encoding, will be required as a minimum to accommodate 256 keys and 256 locks? I think I know the answer, but let's see what the forum comes up with.

-Phil

P.S. If you suggest Manchester (or similar) encoding, each "bit" will count as two bits. Also, the bit widths for 1 and 0 must be the same.

Duane Degn · 2013-12-03 15:20

It seems like any solution would require all "fitting" keys to have the same number of ones. My gut is telling me the number of positions will end up being 16 but I'm not positive about this "yet".

Edit: As I think about this a bit more, I'm betting the answer ends up being less than 16. This calls for someone good at permutations and combinations. It's been awhile since I've done that sort of math.

prof_braino · 2013-12-03 15:55

Can you have a constraint such that locks and keys only accept attempts when they have the same number of 1's?

Phil Pilgrim (PhiPi) · 2013-12-03 16:03

prof_braino wrote:

Can you have a constraint such that locks and keys only accept attempts when they have the same number of 1's?

If such a constraint works out by itself mechanically, then it's okay; but there can be no a priori limitations without a corresponding mechanical one.

-Phil

Duane Degn · 2013-12-03 16:13

I know the answer thanks for a quick Prop program. I was way off.

BTW, if you have enough bits to get 256 locks, you could have 495 locks.

Duane Degn · 2013-12-03 16:16

Oops. I spoke too soon. I realize I assumed the locks would have eight one bits. I'll come back to this later if no one has it (I'd be surprised if no one does).

Phil Pilgrim (PhiPi) · 2013-12-03 16:23

Assuming that the "fixed number of one bits" principle is correct, Pascal's Triangle will provide the answer.

Duane Degn wrote:

BTW, if you have enough bits to get 256 locks, you could have 495 locks.

I get 462 instead of 495. Had I relaxed my requirements to 252, one fewer bit position would've sufficed.

The question then becomes, "Working with fewer bit positions, can you replace some of the "n ones" combinations with larger numbers of "n-1 ones" combinations to buy more total combinations?"

-Phil

Duane Degn · 2013-12-03 16:29

Phil Pilgrim (PhiPi) wrote: »

I get 462 instead of 495. Had I relaxed my requirements to 252, one fewer bit position would've sufficed.

You're right (according to my latest attempt). I get 462 two different ways (same number of total bits). The number of ones and zeros is of course reversible. It doesn't require 8 ones as I had originally assumed.

You allude to a mathematical solution, I just took the brute force approach and tested bits.

Phil Pilgrim (PhiPi) · 2013-12-03 16:40

Just out of curiosity, Duane, how did you arrive at your answer? (I cheated and used a scientific calculator.)

As a result of this exercise, I think my puzzle will have 252 pieces, rather than 256.

But, come to think of it, a straight binary coding may be even more diabolical. I believe that, if one key "fits" a lock incorrectly, that means that when all the other keys are fittted correctly, there will still be one pair left over that does not work. IOW, it's impossible to get ALL of the key/lock pairs mated if at least one was mated the "wrong way." But could you, by mating more than one the wrong way, still get all of them to "fit?" Hmmmm.

-Phil

Duane Degn · 2013-12-03 19:47

Phil Pilgrim (PhiPi) wrote: »

Just out of curiosity, Duane, how did you arrive at your answer? (I cheated and used a scientific calculator.)

I used the tool I use to find all of life's problems, Spin.

CON

  _clkmode = xtal1 + pll16x
  _xinfreq = 5_000_000


OBJ


  Pst : "Parallax Serial Terminal"


PUB Main | oneCount, bit, matchCount, limit, numberToTest, temp, onesInLock


  Pst.start(115200) 
  waitcnt(clkfreq * 2 + cnt)


  repeat onesInLock from 4 to 8
    Pst.Str(string(13, 13, "onesInLock = "))
    Pst.Dec(onesInLock)
      
    repeat result from 8 to 16
      limit := (1 << result) - 1    
      Pst.Str(string(13, "***************   bits = "))
      Pst.Dec(result)
      matchCount := 0 
      repeat numberToTest from 0 to limit
        oneCount := 0
        
        temp := numberToTest
        repeat result
          bit := temp & 1
          if bit
            oneCount++  
          temp >>= 1
     
        if oneCount == onesInLock
          matchCount++
          
      Pst.Str(string(13, "limit = "))
      Pst.Dec(limit)
      Pst.Str(string(13, "matchCount = "))
      Pst.Dec(matchCount)
      if matchCount => 256
        Pst.Str(string(13, "onesInLock = "))
        Pst.Dec(onesInLock)
        quit

Here's the output:

onesInLock = 4
***************   bits = 8
limit = 255
matchCount = 70
***************   bits = 9
limit = 511
matchCount = 126
***************   bits = 10
limit = 1023
matchCount = 210
***************   bits = 11
limit = 2047
matchCount = 330
onesInLock = 4


onesInLock = 5
***************   bits = 8
limit = 255
matchCount = 56
***************   bits = 9
limit = 511
matchCount = 126
***************   bits = 10
limit = 1023
matchCount = 252
***************   bits = 11
limit = 2047
matchCount = 462
onesInLock = 5


onesInLock = 6
***************   bits = 8
limit = 255
matchCount = 28
***************   bits = 9
limit = 511
matchCount = 84
***************   bits = 10
limit = 1023
matchCount = 210
***************   bits = 11
limit = 2047
matchCount = 462
onesInLock = 6


onesInLock = 7
***************   bits = 8
limit = 255
matchCount = 8
***************   bits = 9
limit = 511
matchCount = 36
***************   bits = 10
limit = 1023
matchCount = 120
***************   bits = 11
limit = 2047
matchCount = 330
onesInLock = 7


onesInLock = 8
***************   bits = 8
limit = 255
matchCount = 1
***************   bits = 9
limit = 511
matchCount = 9
***************   bits = 10
limit = 1023
matchCount = 45
***************   bits = 11
limit = 2047
matchCount = 165
***************   bits = 12
limit = 4095
matchCount = 495
onesInLock = 8

I initially didn't have "oneInLock" increment. I started out assuming there would be eight ones.

Duane Degn · 2013-12-03 19:56

I just realized you can make the puzzle work with 4, 5, 6 or 7 ones and stay within the 11-bit limit. 5 or 6 ones yield the maximum number of combinations (462 as you previously stated) which satisfy the requirements on the puzzle.

Franklin · 2013-12-03 22:24

I don't think I understand this. As I see it there are no keys that would fit only one lock.If the lock was all zeros all keys would fit.

kuroneko · 2013-12-03 22:39

Franklin wrote: »

As I see it there are no keys that would fit only one lock.If the lock was all zeros all keys would fit.

You wouldn't use the all-0 lock (or the all-1 key for that matter). IOW not all keys/locks are useful (out of a given range).

Phil Pilgrim (PhiPi) · 2013-12-04 00:17

Franklin wrote:

If the lock was all zeros all keys would fit.

True. But given the puzzle's initial premises, you would not include a lock with all zeroes in the mix.

However, in the more diabolical approach, a lock with all zeroes is okay. If, for example, a key with the value 00000001 were inserted into it, and all the other keys inserted correctly, you'd end up with a 00000000 key that didn't fit the remaining 00000001 lock, and the user (i.e. victim) would have to backtrack to find his/her error. I'm just not sure I want to make the mechanical puzzle that difficult, though. The 5-of-10 code, with 252 possible locks, seems more attractive at the moment, since it does not permit this sort of "garden path" error to occur in the first place.

-Phil

Mark_T · 2013-12-04 00:59

This thread is related to Hamming distance and coding theory - however are these keys able to be used physically reversed?
That alters the problem.

As the design stands its trivial to make a master key, which is undesirable property of a lock design!

Phil Pilgrim (PhiPi) · 2013-12-04 09:32

Mark_T wrote:

As the design stands its trivial to make a master key, which is undesirable property of a lock design!

True. However, in this app, nothing can be unlocked until all 256 keys fit their respective locks, and the user is not given the option of making his own keys. Using a straight binary coding will work, but the user may not know a mistake was made until trying to fit the last key in place. By using a 5-of-10 or 5-of-11 code, it will be impossible to fit a key into the wrong lock. It just depends upon how devious I want to make the physical puzzle.

-Phil

Gadgetman · 2013-12-06 00:54

I'm a bit curious about this Project...
I'm also wondering why the 'keys' need a 'physical fit' like that?

In most locks, you won't know if a key fits before you try to turn it.
but here you end up with keys that can only fit one lock even before 'activation'.

So, Yeah, I'm curious about this one...

Phil Pilgrim (PhiPi) · 2013-12-06 01:14

The key/lock metaphor may have been a little misleading. It's actually more like a jigsaw puzzle, wherein all the pieces have to fit together before it can be deemed "solved." The reason for introducing the key/lock metaphor is that the 3D graphical features of the jigsaw are a bit too subtle to rely upoin exclusively as and aid to solving the puzzle, and I thought some added binary cues might make the puzzle a little less intimidating.

-Phil

Heater. · 2013-12-06 01:41

I presume the intention here is that the keys have a face side and a back side and are to be used face side up.

How would it change things if he keys were allowed to be flipped over, reversing the order of the bits?

When can we buy this puzzle as a box of laser cut plywood keys?

Phil Pilgrim (PhiPi) · 2013-12-06 08:53

heater wrote:

I presume the intention here is that the keys have a face side and a back side and are to be used face side up.

Yes, the "key" teeth are pointing downwards and mate to a frame containing the "locks."

How would it change things if he keys were allowed to be flipped over, reversing the order of the bits?

I'm going to offset the teeth in such a way that that can't happen.

-Phil

Heater. · 2013-12-06 09:34

Or you could make the teeth saw tooth instead of square perhaps.

Gadgetman · 2013-12-06 11:32

Or introduce a groove along one edge or something, so that it will only fit one way around?

Key/Lock Puzzle

Comments