Normal polygons and Circles with ActivityBot
 NikosG
Posts: 705
NikosG
Posts: 705
Helo everybody,
In this thread I will try to explain how we can make polygonal and circular orbits with a deferential robot. I will give you some examples of regular polygons and circles, first using mathematics, and then giving the algorithms which can be implemented in ActivityBot of Parallax and various other robots (like the S2). But first it is necessary to have studied and analyzed the problem of the rotation of every particular robot. We should be able to program the robot to do the right rotations (clockwise or counterclockwise) according the various angles 0 ° < ω < 360 ° that we want to turn.
[size=+2] Rotation of ActivityBot ω degrees [/size]
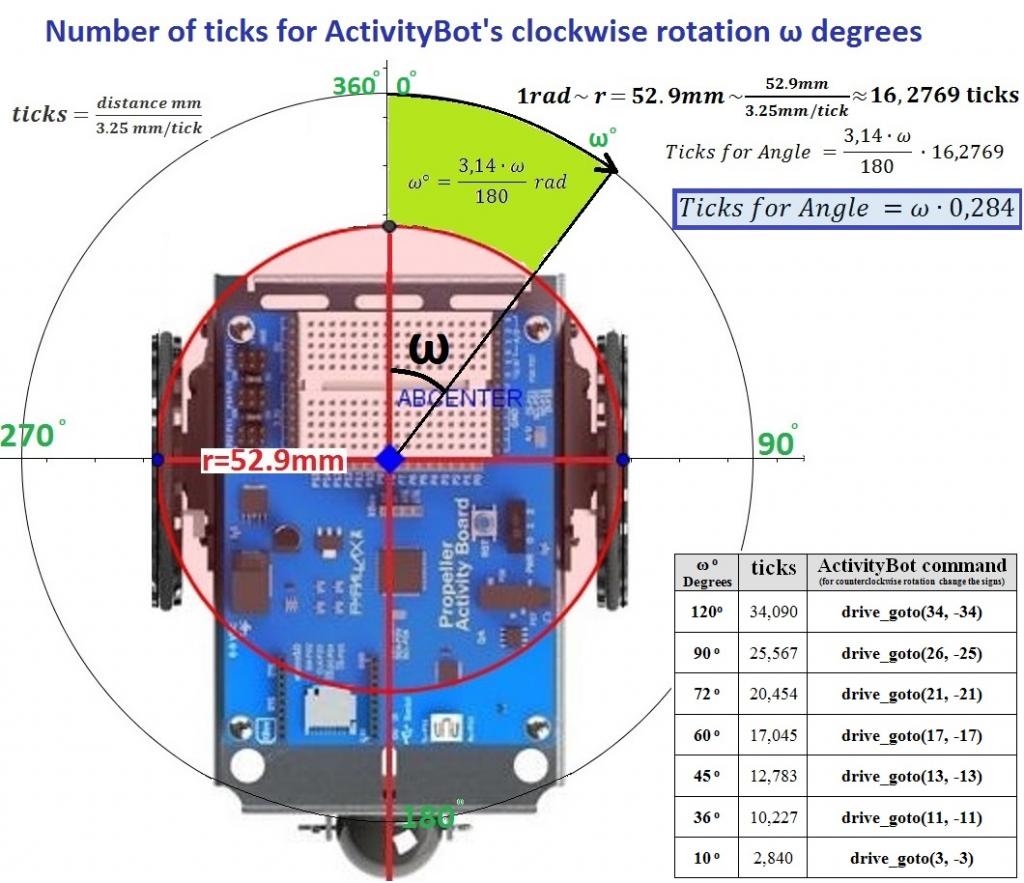
Studying the examples of ActivityBot Navigation you can see that the drive_goto(26, -25) command makes the ActivityBot to execute a 90-degree right turn. Let’s see this example closer and try to create a formula in order to calculates the appropriate “ticks for” this command for a random angle ω.

As the ActivityBot makes a rotation it moves its wheels on the red circle which has radius 52.9mm. If the robot makes a turn equal to 1 rad, each wheel will make a distance equal to the radius r of the red circle. Thus 1 rad rotation of the ActivityBot is equivalent to movement of the wheels at a distance r=52,9mm= 52,91/3,25 ticks= 16,2769 ticks . Changing rad to degrees we take the formula: Ticks for Angle= ω * 0,284. So if we want to program the ActivityBot in order to rotate ω degrees we can multiply by 0,284 in order to find the appropriate wheel ticks.
To verify the above formula we can see that a rotation 90 degrees=90*0.284 ticks=25,56ticks=26 ticks
In the image above, you can also see a useful table with some angles that we will use in the next steps.
[size=+2] Making Polygonal paths using robots[/size]
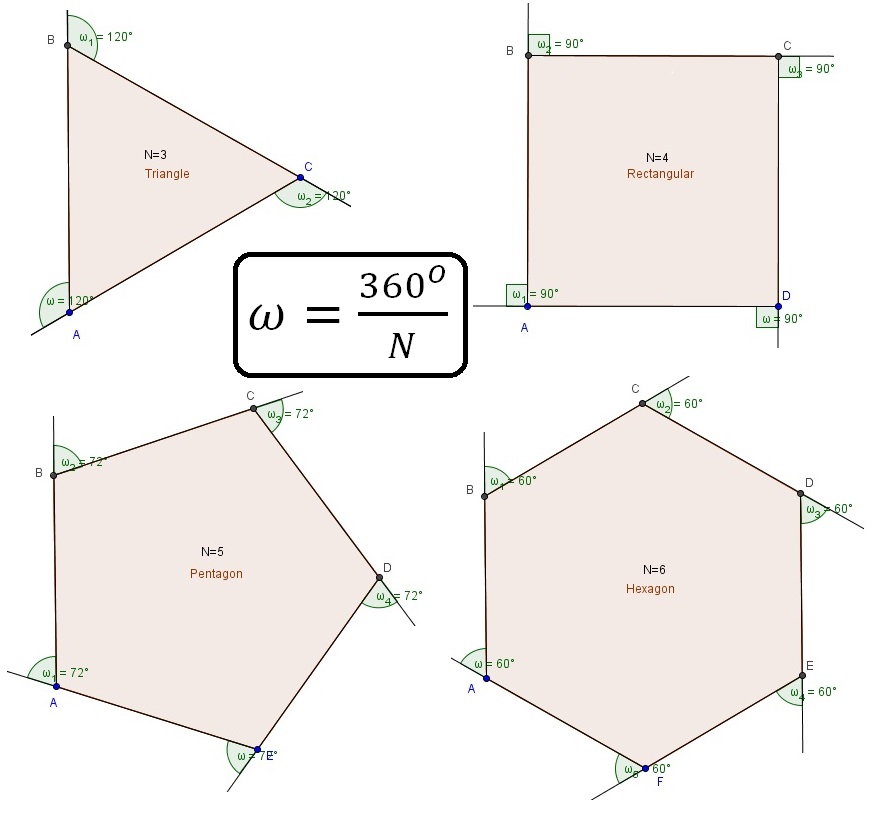
Polygon is a closed shape that has N vertices and N sides (N ≥ 3). Specifically regular polygon is the polygon that has all sides equal.
So some categories of normal polygons for example are:
The equilateral triangle (N = 3 ) , the square (N = 4 ) , the regular pentagon (N = 5), the regular hexagon (N = 6 ) etc.
Normal polygons with (N ≥ 36) have a special interest, because they are practically close to the circle. Although there are not real cycles, in practice these polygons can represent a circle with very good precision.
We will try now to do orbits of regular polygons with the ActivityBot.
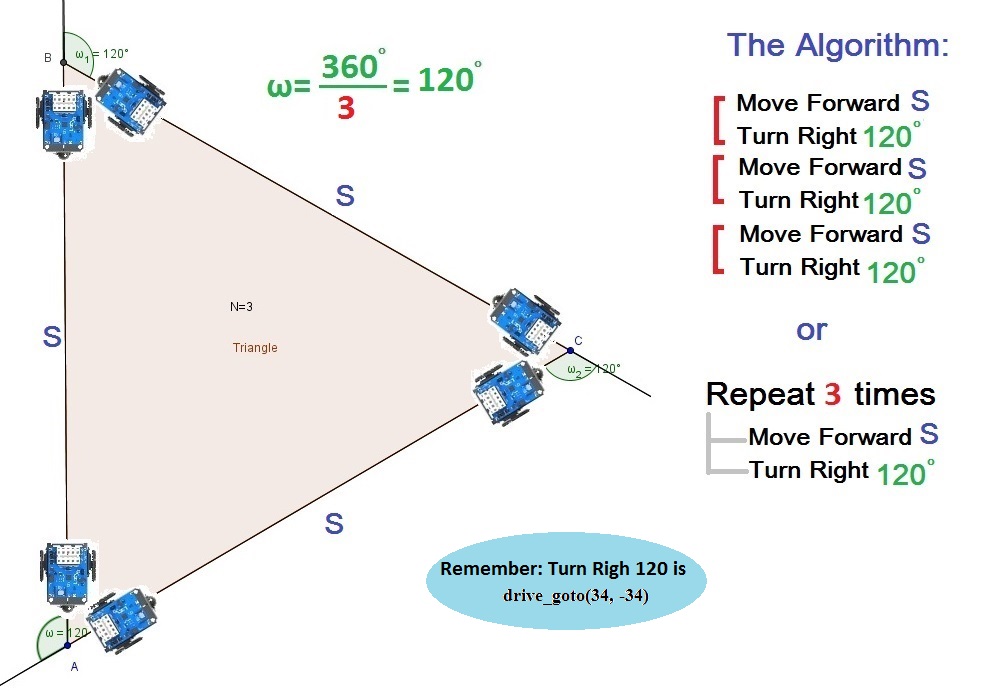
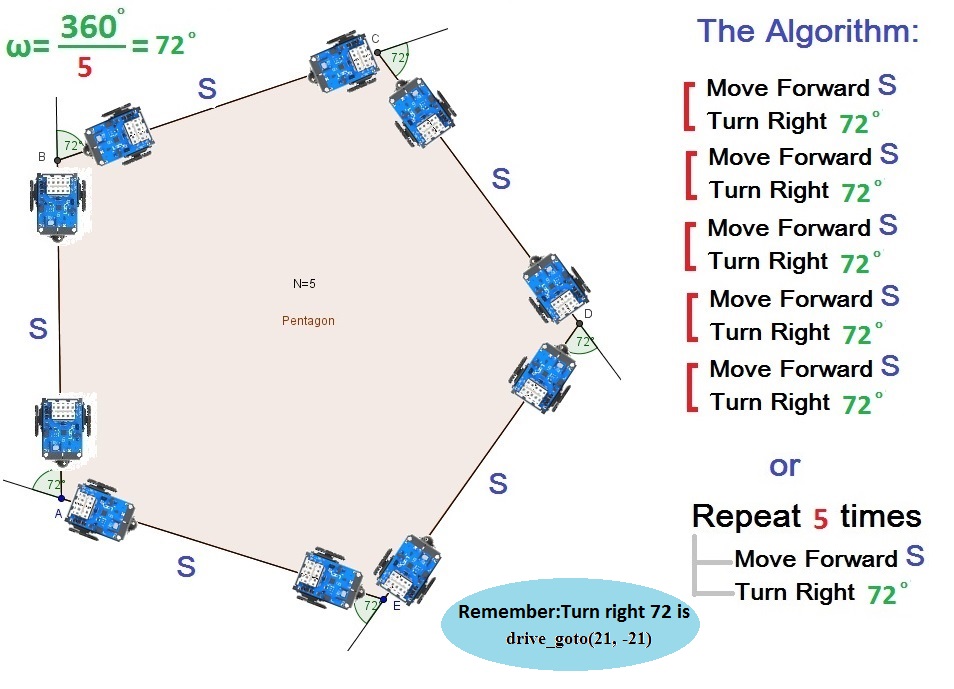
In order to achieve these goals it is essential to know the external angle of the normal polygon in order to give the robot the appropriate command to turn properly. The external angle ω , of a normal polygon (n>=3) is given by the formula: ω=360/N

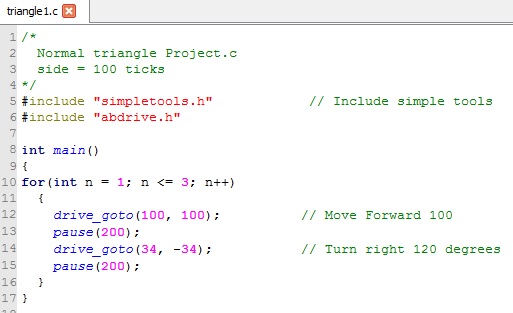
So in order to make (clockwise) an equilateral triangle with side S, using the ActivityBot we must give the following commands:

The SimpleID code is:

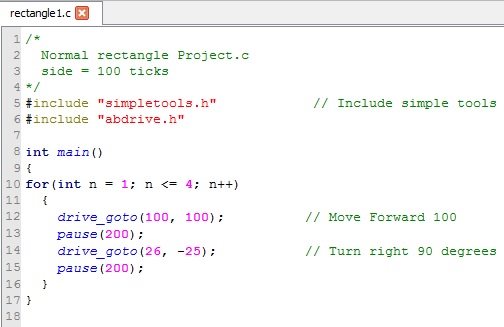
If we want the robot to do a square path of side S (clockwise) we need to give the following commands:

The SimpleID code is:

If we want the robot to do a normal pentagon path of side S (clockwise) we need to give the following commands:

The SimpleID code is:

We can give a general algorithm for every normal polygon with N vertices (Ν≥3) and side S (clockwise):

Nikos Giannakopoulos
In this thread I will try to explain how we can make polygonal and circular orbits with a deferential robot. I will give you some examples of regular polygons and circles, first using mathematics, and then giving the algorithms which can be implemented in ActivityBot of Parallax and various other robots (like the S2). But first it is necessary to have studied and analyzed the problem of the rotation of every particular robot. We should be able to program the robot to do the right rotations (clockwise or counterclockwise) according the various angles 0 ° < ω < 360 ° that we want to turn.
[size=+2] Rotation of ActivityBot ω degrees [/size]
Studying the examples of ActivityBot Navigation you can see that the drive_goto(26, -25) command makes the ActivityBot to execute a 90-degree right turn. Let’s see this example closer and try to create a formula in order to calculates the appropriate “ticks for” this command for a random angle ω.
As the ActivityBot makes a rotation it moves its wheels on the red circle which has radius 52.9mm. If the robot makes a turn equal to 1 rad, each wheel will make a distance equal to the radius r of the red circle. Thus 1 rad rotation of the ActivityBot is equivalent to movement of the wheels at a distance r=52,9mm= 52,91/3,25 ticks= 16,2769 ticks . Changing rad to degrees we take the formula: Ticks for Angle= ω * 0,284. So if we want to program the ActivityBot in order to rotate ω degrees we can multiply by 0,284 in order to find the appropriate wheel ticks.
To verify the above formula we can see that a rotation 90 degrees=90*0.284 ticks=25,56ticks=26 ticks
In the image above, you can also see a useful table with some angles that we will use in the next steps.
[size=+2] Making Polygonal paths using robots[/size]
Polygon is a closed shape that has N vertices and N sides (N ≥ 3). Specifically regular polygon is the polygon that has all sides equal.
So some categories of normal polygons for example are:
The equilateral triangle (N = 3 ) , the square (N = 4 ) , the regular pentagon (N = 5), the regular hexagon (N = 6 ) etc.
Normal polygons with (N ≥ 36) have a special interest, because they are practically close to the circle. Although there are not real cycles, in practice these polygons can represent a circle with very good precision.
We will try now to do orbits of regular polygons with the ActivityBot.
In order to achieve these goals it is essential to know the external angle of the normal polygon in order to give the robot the appropriate command to turn properly. The external angle ω , of a normal polygon (n>=3) is given by the formula: ω=360/N
So in order to make (clockwise) an equilateral triangle with side S, using the ActivityBot we must give the following commands:
The SimpleID code is:
If we want the robot to do a square path of side S (clockwise) we need to give the following commands:
The SimpleID code is:
If we want the robot to do a normal pentagon path of side S (clockwise) we need to give the following commands:
The SimpleID code is:
We can give a general algorithm for every normal polygon with N vertices (Ν≥3) and side S (clockwise):
Nikos Giannakopoulos





Comments
BTW, Nikos, have you seen the latest S2 GUI (beta) build with the Greek language translation? If not, give me your email address, and I'll send it to you.
-Phil
Phil, Nikos, I posted it here: http://www.parallax.com/downloads/s2-gui-software
-Phil
I have already installed the GUI-v1.4 Beta on School's new lab in order to use it in my class.
This Lab has Ubuntu as operating system but the server has also windows. I succesfuly installed the new GUI on server under windows and I can also share the application on the other terminal computers. However I haven't test the software using the robot. In the past I had some problems because many times I couldn't upload programs on my S2.(I suppose it was a driver issue)
I'll test it again now and I'll send you a feedback.
@Phil,
I'm trying to find a way to turn the S2 in a specific angle using the motion tile icon on GUI, in order to make normal polygons using my S2.
I think that GUI doesn't help very much in this point. I think that the only way to approach a speciffic angle in this way is to calculate the time for this speciffic angle. Have I right? Is any other way to achieve this goal using the GUI?
Nikos.
Hi Nikos,
I am not sure that you can program the S2 from a Linux terminal and Windows server with the Propeller Tool (which is utilized by the GUI). I know that we usually recommend local installation. I will check into that.
-Phil
The Propeller Tool should be able to work from a networked installation, but I wouldn't be able to guarantee that it works for Propeller programming (downloading) via a connected terminal where the Propeller is physically connected.
How is the terminal connection made? Some kind of Windows emulation? If so, have you tried locally installing the Windows USB drivers? http://www.parallax.com/downloads/parallax-usb-driver-installer
That is an awesome post! Thanks so much for the information. This is great for students all around the world..
Jim
As we said before, circle has a special interest because we can approach it with a normal polygon with 36 vertices.
So, if we want the robot to do a circle (clockwise) we need to give the following commands:
Have in mind that the S mustnt be a big number because circle will be huge!
At this point choose for S small numbers. For instance in the next example the S= 8 ticks.
The following SimpleID code programs the ActivityBot in order to make a circle with radius 15cm approximately:
The question that arises is: how much should be the S in order to take a circle with a specific R? In other words can I calculate the S as a function of R?
Math theory gives the answer again with the Cosines Law. Looking at the triangle OA1A2 we can see that:
At this point we are almost ready for the final algorithm that will be able to create any circles with a given radious r and ofcourse any other normal polygon isnide this circle.
Nikos Giannakopoulos
Jeff,
The terminal connection now in my Lab is a kind of Windows emulation. In the past (before the Ubuntu instalation ) I had only Windows. However I had many problems with the drivers. (I had installed them many times from the link you said before but always I had problem and I used my notebook in order to load the programs into S2)
Thanks for sharing.
How we can I do this in practice using the GUI ? Must I write a subroutine?
For example, to turn 90 degrees, Spd * MoveTime = 90 * 1111.1111 = 100_000
Setting Spd to 100 and MoveTime to 1 sec (1000 ms) should do the trick. Of course, not all angles will work out so nicely, given the 50 ms granularity of the times.
-Phil
Can you confirm for me, please, whether the newly-added Unicode capability and consequent Greek translation are working properly for you? IIRC, there might be a couple holes in the file greek.dic that still need to be filled with correct translations.
Thanks,
-Phil
Phil
The Greek Translation of the GUI is very good !
I can assure you that everyone Greek user can understand the meaning . In addition the icon of each command is perfect and explains the meaning without words.
However If you want to do a more "Greek" translation here is a screenshot with some small changes:
Phil ,
if I could make a suggestion for the GUI, This would be about the motion tile icon. I think that will be very helpful if users could have the choise to turn the wheels specific number of rotations 1,2,3...etct or specific degrees (360 degrees=1 rotation). (something like the Lego NXT motor command)
Thanks for the feedback on the Greek translation. There's a file that comes with the GUI, greek.dic (in the same folder as s2.exe). Would you be willing to take a look at that file, edit it with the better translations, and email it to me?
Also, I like your suggestion about the motion tile. I will have to figure out a way to do it that doesn't break existing GUI programs.
Thanks,
-Phil
The flowchart that describes the final algorithm in order to do a circle with given R is the following:
This algorithm works also well and for all the other normal polygons
As you can see the program can also make your ActivityBot to do any normal polygon inside a circle with a radius r.
Here are some polygons and circle that you can make with your AcrivityBot changing the values of variables n, r on the above code.
As a small improvement of the above code we can change it in order to make the circles and the polygons, clockwise or counterclockwise according to our needs.
Nikos Giannakopoulos
We can make calculation easier using the Excel.
At the end of the post I provide a spreadsheet that can help. So here is a table with some of the angles we use in order to draw normal polygons and circles using the S2
Following the algorithms that I mentioned on Post #1 we can make:
A triangle:
A square:
A normal pentagon:
A normal hexagon:
A circle:
The attached file "S2_polygons_code" has also the code for your S2.
Nikos Giannakopoulos
http://gianakop.blogspot.gr/2014/02/blog-post.html
Greek students and teachers, will also have the opportunity to admire the s2 robot drawing normal polygons and many other drawings, in our presentation (me and with my students) on 4th Students Festival in Patras that will take place on 1rts General Lyceum of Patras on 3-4 of April 2014.
Nikos Giannakopoulos