Dog-leg hypotenuse approximation
For reasons that may never become clear, I needed a fast approximation to the hypot function, calculating the length of the hypotenuse given the length of the other two sides of a right triangle. Here were my requirements:
hi = max( a, b )
lo = min( a, b )
hypot ~= hi + lo/2
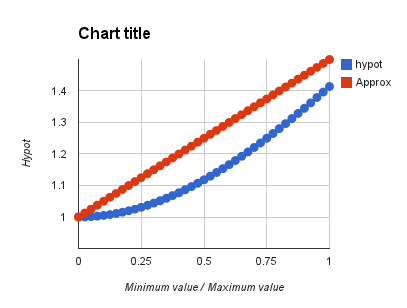
(Note that I am using 'max' and 'min' in the C sense, not the Propeller sense.) This is extremely fast, and not too horrible. To test this out, I made a spreadsheet with a graph, a RMSE calculation, and a worst error calculation. I normalized the maximum value to 1.0, and ran the minimum value from 0 up to 1. I'm attaching the spreadsheet.
I found that the simple hi+lo/2 approximation had a worst case error of ~11.8%, and the estimate was always high. By changing the multiplier on the lo term to 0.33 you could minimize the RMSE of the approximation. If your processor has integer division, hi + lo/3 is your best bet for this (max error ~5.7%). Since I am doing this in PASM, I found 3/8 to be the best approximation for me (3 adds and a shift @ ~6.8% max error). Note that you can reduce the RMSE further by allowing the gain of the hi term to be < 1.0 (hypot ~= 0.936*hi + 0.426*lo), but I have some reasons for not doing that and the worst error is still 6.4%.
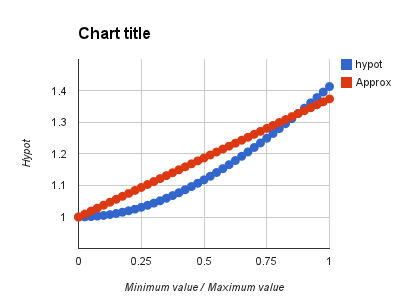
I was thinking given the shape of the curve, a piece-wise linear function would do a better job than the straight linear function...something with a dog-leg in it (bent somewhere in the middle). It occurred to me that the function max( 0, N*lo - hi) should work. E.g., if N==2, when lo < hi/2, the term will be clamped to z, and when above hi/2 it will be linear. So the form of the new equation is:
hypot ~= hi + Gain_lo * lo + Gain_dogleg * max( 0, N * lo - hi )
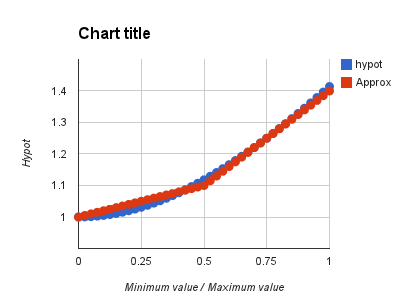
For N = 2, the best (integer operation) gains turned out to be = 1/5. So if you have integer division you could say:
hypot ~= hi + (lo + max( 0, lo+lo-hi ) ) / 5
(max error is ~2.0%)
However, the best solution I found with just shifts and adds was this:
hypot ~= hi + (lo + max( 0, lo+lo+lo-hi ) ) / 8
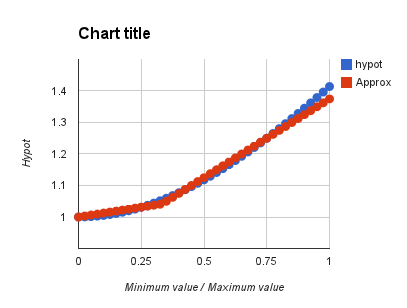
The max error is ~2.8%, and it only takes 11 PASM instructions, including the 3 to sort into hi and lo.
thanks,
Jonathan
- works with integers larger than 16-bit
- doable in Propeller Assembly
- FAST
- reasonably accurate
hi = max( a, b )
lo = min( a, b )
hypot ~= hi + lo/2

(Note that I am using 'max' and 'min' in the C sense, not the Propeller sense.) This is extremely fast, and not too horrible. To test this out, I made a spreadsheet with a graph, a RMSE calculation, and a worst error calculation. I normalized the maximum value to 1.0, and ran the minimum value from 0 up to 1. I'm attaching the spreadsheet.
I found that the simple hi+lo/2 approximation had a worst case error of ~11.8%, and the estimate was always high. By changing the multiplier on the lo term to 0.33 you could minimize the RMSE of the approximation. If your processor has integer division, hi + lo/3 is your best bet for this (max error ~5.7%). Since I am doing this in PASM, I found 3/8 to be the best approximation for me (3 adds and a shift @ ~6.8% max error). Note that you can reduce the RMSE further by allowing the gain of the hi term to be < 1.0 (hypot ~= 0.936*hi + 0.426*lo), but I have some reasons for not doing that and the worst error is still 6.4%.

I was thinking given the shape of the curve, a piece-wise linear function would do a better job than the straight linear function...something with a dog-leg in it (bent somewhere in the middle). It occurred to me that the function max( 0, N*lo - hi) should work. E.g., if N==2, when lo < hi/2, the term will be clamped to z, and when above hi/2 it will be linear. So the form of the new equation is:
hypot ~= hi + Gain_lo * lo + Gain_dogleg * max( 0, N * lo - hi )
For N = 2, the best (integer operation) gains turned out to be = 1/5. So if you have integer division you could say:
hypot ~= hi + (lo + max( 0, lo+lo-hi ) ) / 5
(max error is ~2.0%)

However, the best solution I found with just shifts and adds was this:
hypot ~= hi + (lo + max( 0, lo+lo+lo-hi ) ) / 8

The max error is ~2.8%, and it only takes 11 PASM instructions, including the 3 to sort into hi and lo.
hypot ' fast hypotenuse approximation
' first sort into max and min
mov vRes, v1
min v1, v2
max v2, vRes
' now that v1 = max, and v2 = min
' Dog-Leg approximation N=3, 2.8% error
' do the dog-leg term (1/3 of the way in)
mov vRes, v2
add vRes, v2
add vRes, v2
sub vRes, v1
mins vRes, #0 ' clamp the dog-leg term
add vRes, v2 ' add in the linear term
shr vRes, #3 ' scale by 1/8th
add vRes, v1 ' add in the max term
hypot_ret ret
I welcome any optimizations or comments, and hopefully this is useful to someone.thanks,
Jonathan



Comments
hypot ~= hi + 3*lo/32 + max(0,2*lo-hi)/8 + max(0,4*lo-hi)/16
(worst error is ~0.77%)
Here's the shortest PASM code I could find so far (18 instructions), and it requires extra scratch variables, so I really appreciate any possible improvements!
hypot ' fast hypotenuse approximation ' first sort into max and min mov vRes, v1 min v1, v2 max v2, vRes ' now that v1 = max, and v2 = min ' Double-Dog-Leg approximation, 0.8% error ' hypot ~= hi + 3*lo/32 + max(0,2*lo-hi)/8 + max(0,4*lo-hi)/16 ' alternatively ' hypot ~= hi + 3*lo/32 + (max(0,2*lo-hi) + max(0,2*lo-hi/2) )/8 mov vRes, v1 shr v1, #1 mov tmp, v2 add tmp, v2 add v2, tmp shr v2, #5 add vRes, v2 sub tmp, v1 mins tmp, #0 mov tmp1, tmp sub tmp, v1 mins tmp, #0 add tmp1, tmp shr tmp1, #3 add vRes, tmp1 hypot_ret retthanks,Jonathan
Oh I am intrigued as to the reason - though I can't see why a general table-lookup linear interpolation won't serve your purpose more flexibly.
One reason I've done this is using integer arithmetic to calculate CNC stepper drive signals - the hypotenuse is needed to drive the speed feedback
DDA - am I close?
RAM is precious, I don't think I could fit a table in right now. How would you do a table implementation without at least one scaling division? This only costs me 72 clocks atm, and of course I'd love to reduce that. [8^)
Jonathan
http://danielnouri.org/docs/SuperColliderHelp/BinaryOps/hypotApx.html
Note that it's a tough gain to approximate with integer math, and of course the worst case error (~8.2%) and the RMSE are both worse than the 3/8 gain linear form. The dogleg form is different and superior. The double-dogleg form is even more so. [8^)
EDIT: I take that back...either that equation as presented has some typos, or their approximation is much worse (15.9%!). I think I charted what they *meant* to do.
Jonathan
Divide the distance you've run (longer side) into 8 equal parts and discard one part from it. Then if you add the half the height to that, you'll get Hypotenuse.
That is like your first approximation,
hypot ~= hi + (lo + max( 0, lo+lo+lo-hi ) ) / 8
in the region where the max(0, lo+lo+lo-hi ) is positive. There it reduces to
hypot ~= hi + 4*lo/8 - hi/8 = 7*hi/8 + lo/2.
Your dog-leg condition max(.,.) is much better though--You have indeed surpassed the ancients!
I plotted the values with and without the dogleg along with the true sqrt(x^2+y^2). In this rendition the total length is constrained to x+y=1.
Looking at the graph it seems we need to do half of the dog leg at one end of the scale and replace the other half of the dog leg with tamil poetry where it fits very well.
I'm curious, what's the reason for all the hypontenuse working in PCB layout?
Back in the day I worked on a PCB design package, CADSTAR. It had auto-placement and I seem to remember it got better results when it used the Manhattan distance between connected points rather than the "as the crow flies" distance. Hence my curiosity.
To this day I have never come across a PCB designer that said he used any kind of auto-place so I often wondered why we bothered:)
PS According to wiki, the Tamil for hypotenuse is
Jonathan
* Or, for you Keanu Reeves fans, "Dogstar".
hypot ' fast hypotenuse approximation ' first sort into max and min mov vRes, v1 min v1, v2 max v2, vRes ' now v1 = max, and v2 = min ' Double-Dog-Leg optimized approximation, 0.8% error ' hypot ~= hi + 3*lo/32 + max(0,2*lo-hi)/8 + max(0,4*lo-hi)/16 ' rewritten as ' hypot ~= 3*lo/32 + hi + max(0,lo/4-hi/16) + max(0,lo/4-hi/8) ' gain_lo mov vRes, v2 add vRes, v2 add vRes, v2 shr vRes, #5 ' gain_hi add vRes, v1 ' scale the sides for the dogleg calcs shr v1, #4 shr v2, #2 ' 1/4 dogleg sub v2, v1 mins v2, #0 add vRes, v2 ' 1/2 dogleg sub v2, v1 mins v2, #0 add vRes, v2 hypot_ret retMake sure you either use absolute values (or intentionally use 32-bit unsigned values, though the '3 * lo' term may overflow).Jonathan
Ive been working on a light-weight FPGA graphics engine for a small screen, and I needed a distance approximation to be cheap and fast in hardware. The long + (short>>1) approximation is all anyone seems to reference, but it isnt accurate enough to use to draw circles (for example).
I started down the path of a LUT approach, but I couldnt afford it because it would take a division to normalize. I needed to avoid multiplication if at all possible, as well. Your 0.77% version gets around all that and manages to look good in my applications. Its light enough to calculate a distance result on each clock cycle. Basically, that approach is exactly what I needed.
The whole thing strikes me as really clever.
longerside + shorterside*3/8
I believe the max error is 5.3%. The 3/8 is some right-shifts and adds.
I thought I'd try that out in Tachyon and passed it through that method and your normal calculation and had it report some results (just using trimmed values from memory as "random" data)
[FONT=courier new][COLOR=#000000]pub [/COLOR][COLOR=#000000][B]HYPOT[/B][/COLOR][COLOR=#000000] ( A B -- hypot )[/COLOR][/FONT] [FONT=courier new][COLOR=#000000] 2DUP < IF SWAP THEN[/COLOR][/FONT] [FONT=courier new][COLOR=#000000] DUP DUP + + 3 SHR + \ *3/8[/COLOR][/FONT] [FONT=courier new][COLOR=#000000] ; [/COLOR][/FONT] [COLOR=#9900ff][FONT=Ubuntu Mono]pub HDEMO ( addr -- )[/FONT][/COLOR] [COLOR=#9900ff][FONT=Ubuntu Mono] $40 DECIMAL[/FONT][/COLOR] [COLOR=#9900ff][FONT=Ubuntu Mono] ADO I W@ $7FFF AND I 2 + W@ $7FFF AND[/FONT][/COLOR] [COLOR=#9900ff][FONT=Ubuntu Mono] CR OVER .DEC TAB DUP .DEC [/FONT][/COLOR] [COLOR=#9900ff][FONT=Ubuntu Mono] TAB ." APPROX HYPOT=" 2DUP HYPOT DUP 0 REG ! .DEC TAB[/FONT][/COLOR] [COLOR=#9900ff][FONT=Ubuntu Mono] ." HYPOT = " ^2 SWAP ^2 + SQR DUP .DEC[/FONT][/COLOR] [COLOR=#9900ff][FONT=Ubuntu Mono] DUP 0 REG @ - ABS #10000 * SWAP / \ calulate % error scaled to 2 decimal places TAB ." ERROR=" <# # # "." HOLD #S #> PRINT$ ." %"[/FONT][/COLOR] [COLOR=#9900ff][FONT=Ubuntu Mono] 4 +LOOP[/FONT][/COLOR] [COLOR=#9900ff][FONT=Ubuntu Mono] ;[/FONT][/COLOR] [FONT=courier new] [/FONT]Here's some outputEDIT: added % error function to demo and output
Yeah, 6.8% matches the error I reported using 3/8 in the first post...dividing by 3 was better (~5.7%), but of course required a division.
Jonathan
DDLhypot '' Double Dogleg Hypotenuse approximation ' hypot ~= 3*lo/32 + hi + max(0,4*lo-hi)/16 + max(0,2*lo-hi)/8 ' ** refactored as ** ' hypot ~= (lo/4)*3/8 + hi + max(0,lo/4-hi/16) + max(0,lo/4-hi/8) ' make sure v1 >= v2 mov vRes, v1 min v1, v2 max v2, vRes ' Hypot = (lo/4)*3/8 shr v2, #2 ' pre-dividing makes sure the *3 will not overflow mov vRes, v2 add vRes, v2 add vRes, v2 shr vRes, #3 ' hypot += hi add vRes, v1 ' hypot += max(0,lo/4-hi/16) shr v1, #4 ' sub v2, v1 WC if_NC add vRes, v2 ' hypot += max(0,lo/4-hi/16-hi/16) if_NC sub v2, v1 WC if_NC add vRes, v2 DDLhypot_ret retI also pre-divided the 'lo' term so the 3*lo/32 can not possibly overflow. The function should work as long as the input and output values all fit inside 32-bit unsigned integers. This version weighs in at 14 instructions (not counting call and return) and has the same 0.8% max error (more if you use tiny integers, since it's an integer approximation, for example the hypotenuse of a 1x1 right triangle would yield 1).thanks,
Jonathan
This could also be used for AM demodulation in software defined radios. In this context it's usually called magnitude or (complex) absolute value. And in other contexts, L2 norm.