Pi is wrong?
 Heater.
Posts: 21,230
Heater.
Posts: 21,230
I know a lot of people here are deep into electronic engineering and/or physics and/or maths. So this may be of interest.
As you will all know the number Pi crops up all over the place and is used in equations describing all sorts of things from the area of the circle, to the frequency of an LC resonant circuit to quantum mechanics.
The simple idea here is that the mysterious, magical almost sacred number Pi is actually wrong! Or at least the wrong number to hold in high regard when dealing with circles.
The suggestion is that instead of using a circles circumference and diameter to define the "circle constant", Pi = C/D, we should instead focus on the value of the circles radius and use C/R. Which gives an number twice as big (2Pi) to be called "Tao".
The effect of this is that if you rotate by a full turn (360 degrees) you have rotated one Tau radians. A rotation of a half turn is Tau/2 radians. A rotation of a quarter turn is Tau/4 and so on.
This has a huge simplifying effect on all that early trigonometry stuff you do at school and it gets rid of all those twos you see in millions of equations in science and maths as 2Pi.
On the one hand this seems like a trivial and pointless idea. On the other hand it seems to focus your mind on rotations a lot more naturally. It really makes you wonder how we have landed on Pi as the fundamental number when clearly it is not, after all a lot of very clever people have been doing this for such a long time.
If nothing else the videos found at the following link are really wonderful.
http://tauday.com/
What does everyone here think?
As you will all know the number Pi crops up all over the place and is used in equations describing all sorts of things from the area of the circle, to the frequency of an LC resonant circuit to quantum mechanics.
The simple idea here is that the mysterious, magical almost sacred number Pi is actually wrong! Or at least the wrong number to hold in high regard when dealing with circles.
The suggestion is that instead of using a circles circumference and diameter to define the "circle constant", Pi = C/D, we should instead focus on the value of the circles radius and use C/R. Which gives an number twice as big (2Pi) to be called "Tao".
The effect of this is that if you rotate by a full turn (360 degrees) you have rotated one Tau radians. A rotation of a half turn is Tau/2 radians. A rotation of a quarter turn is Tau/4 and so on.
This has a huge simplifying effect on all that early trigonometry stuff you do at school and it gets rid of all those twos you see in millions of equations in science and maths as 2Pi.
On the one hand this seems like a trivial and pointless idea. On the other hand it seems to focus your mind on rotations a lot more naturally. It really makes you wonder how we have landed on Pi as the fundamental number when clearly it is not, after all a lot of very clever people have been doing this for such a long time.
If nothing else the videos found at the following link are really wonderful.
http://tauday.com/
What does everyone here think?


Comments
The Tauists would say you have that backwards and that Pi = Tau / 2 in the same way we have the number 1 instead of talking about 2 * h, say, where h is a half. In that light Pi starts to look not just inconvenient to use but positively stupid.
So we have PI := Tau >> 1
mindrobots,
Did you notice how Michael Hartl had actually memorized Pi to 50 places and then had to go on to memorize Tau to 50 places!
On seeing that I started to take the guy very seriously.
If you give a child a pair of compasses and some paper and ask them to draw a circle you will probably very soon have a nice circle on the paper.
Then you can suggest that they can construct a hexagon by stepping around the circle with the compasses set to the same distance as used for the radius of the circle.
You might then ask them "how long is the line around the outside hexagon?" They might likely count the straight lines around the outside of the hexagon and come up with answer 6.
You might then ask them "How long is the line around the outside of the circle?" With a bit of head scratching they might come up with an answer like "six and a bit" having realized it's a bit longer to go around the circle that the straight edges of the hexagon.
Clearly that "six and a bit" is a ton more fundamental than Pi.
You see how deep seated this problem is.
Phi2Pi?
PhiTau/2
Tl;dr these Tauist are heretics. Let's gather the pitchforks and torches.
When very young in school we were learning simple arithmetic and using it to find the areas of squares, rectangles and triangles.
At some point the young Heater put his hand up in class and asked "Please Sir, how do we find the area of circles?". Obvious question as we had been messing around drawing circles recently as well.
The answer I got was very frustrating and included statements that this was a very complicated thing that we would learn in high school and that it involved this unspecified and mysterious number Pi. That is to say no answer at all.
I now see that in the time that the teacher took to say all the above he could of gone through the procedure I outlined previously and we would have come up with the answer "six and a bit times the radius". An answer that:
a) Is an answer instead of a frustrating non-answer.
b) Is close enough to the correct result that we would have been happy enough at the time.
c) Plants the idea of the "circle constant" in our minds even if only as a very approximate value, six and a bit.
I have long held the idea that a lot of mathematics contains really dead obvious ideas, that the problem is that the notation gets in the way. One ends up blinded by symbols and can't see the idea underneath it all. This Pi vs Tau thing is an outstanding example of that.
Indeed that feels right.
But in the case of a circle the easiest way to construct one is to start from a radius and sweep it around. As in my procedure previously. The width or diameter never enters into it. Pulling the diameter into it just complicates things.
So when teaching young children, who have never heard of a radius or a diameter or a circumference or an area, what is the easiest approach?
This goes on up through later education in trigonometry, for example why have the zero point of sine at Pi/2 radians? Isn't more obvious that it is at one quarter of a turn or Tao/4 radians?
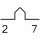
Know pi. Love pi. Pi is never wrong. I had it memorized to 50 places back in 6th grade. Now kids know it much further. We shall be prepared after the Atomic Flame Deluge wipes all recorded knowledge. But scoffers like Rick will have to beg for anything beyond 22/7!
I think you should just throw in the tau.
C.W.
I'm sure there's a species out there somewhere that does something like that. You know, the universe is a big place.
http://www.thepimanifesto.com/
This talk of pi is making me hungry.
C.W.
After reading the Tau Manifesto, I too became a believer in Tau.
electronics I don't see them. Pretty much every time I see a Pi I see a 2 in front of it.
This is bugging me now because I was challenged here to create an "Idiots Guide to the Fast Fourier Transform" . Getting rid of all those unnecessary 2's helps. Next I have to get rid of all those unnecessary i's.
Pecan halves used in PI is a matter of convention and convenience. I prefer the Pecans to be chopped in little pieces.
Of course there is only so many practical ways to slice Pecan PI. Pecan PI/(n^2) is easier to do than PI/6 for example,
Generally I think 2*PI are always better than one.
I miss Pecan PI
I hear slices of that PI are in great demand.
[quote)
Why not define the number 1 as Pi, or Pi/2, and then redefine the universe in terms of that?
[/quote]
There has been at least one attempt to redefine Pi as 3. This kind of thing is obviously nuts.
That is missing the point here. It's not that the value of Pi, as defined, is wrong but rather it's not the fundamental number of interest.
For example, all throughout mathematics we see the number "e". It has been reduced to it's minimal form. We don't see "2e" all over the place.
(Don't they have ANY good Pecan Pi in California???)
Now, which one do you want?
I sense that you guys are not taking this seriously:)
I'm afraid I take Pi for granted much like air....it's there when I need it but I don't obsess over it's composition and properties and in the grand scheme of things I can do little about it's quality except change locations or change my diet.
I might ask, when was the last time you needed to calculate something using Pi and did remembering the extra 2 that you always need help or not?
Pi is not defined as the quantity 3.14... It is the ratio of a circle's circumference to its diameter. It's kind of built in to the universe as we know it.
It does appear that referencing to the radius may be a better idea.
This is true in the realm of mathematics and perfectly flat planes. But it is not true in the real universe as space is not flat, it curved by mass. In addition moving objects experiences length contraction in the direction of motion, which effects the geometry of objects to observers in a different frame of reference.
So any material with mass distorts space enough that it alters the circumference / diameter ratio. An extreme example would be a black hole. We can know its circumference, but we can't measure its radius. We can say what the radius looks like to us, but inside space is curved and stretched.
Suppose I was holding up a picture of a circle and flew by the Earth, while Heater took my picture with a ultra super high speed camera. From Heater's point of view I would be holding an ellipse, not a circle. Now from my point of view I'm still holding a circle, but I am also squished in the direction of my motion.