Shop OBEX P1 Docs P2 Docs Learn Events
Any experts on gears? — Parallax Forums

Any experts on gears?

T ChapT Chap Posts: 4,223
edited 2012-06-12 07:49 in General Discussion
I need to do a 2:1 ratio gear, probably out of Delrin or hi durometer rubber, 1/2" stock. I have a fixed dimension for the shaft centers of 2.125", using 12mm shafts.

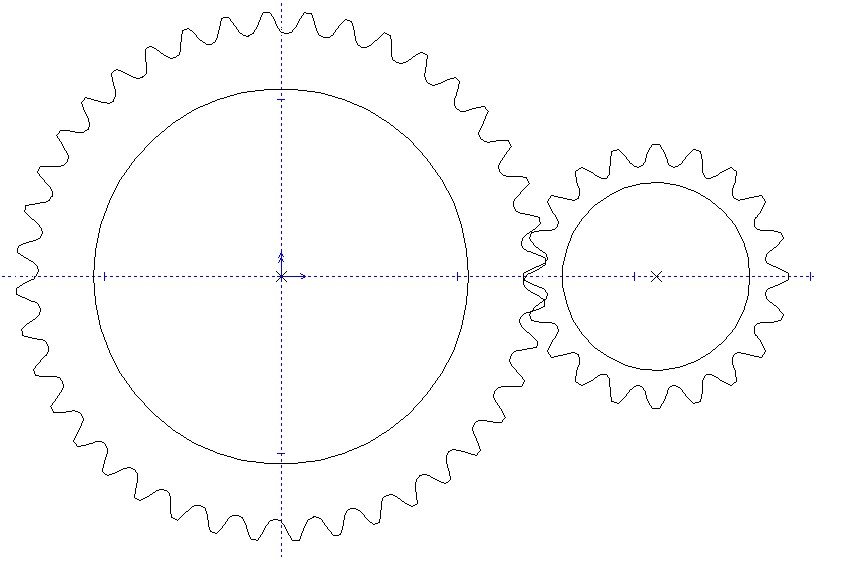
So the gears must be such that one gear has twice as many teeth. I have a program called Bobcad that has a gear creator, but it expects you to know something about how to use it for the specific role. I want to make the teeth fit each other, and have only experimented an hour or so and you can see what I am up against. I have looked online and cannot find a calculator that would output the pitch diameter, outer diameter, root diameter etc for this purpose of a gear box. If anyone has done something like this I could use some advice on how to calculate it.
gears.jpg
860 x 566 - 55K

Comments

  • Phil Pilgrim (PhiPi)Phil Pilgrim (PhiPi) Posts: 23,514
    edited 2012-06-08 16:03
    The pitch diameters are the only things you need to calculate, and they're 2 * 2.125 / 3 for the small gear and 4 * 2.125 / 3 for the large one. Then pick an even number of teeth for the big gear and half that for the little one. Everything else should just come out in the wash.

    -Phil
  • jdoleckijdolecki Posts: 726
    edited 2012-06-08 16:29
    Are you planning on making your own gears?

    Is 2.125 for the shaft centers and locked number?

    servocity.com

    has gears.
  • ScopeScope Posts: 417
    edited 2012-06-08 16:55


    I just purchased the gear generator - by far, the best $26 I've ever spent:

    http://woodgears.ca/gear/

    Also, consider watching the videos about the gear generator software - very impressive:

    http://woodgears.ca/gear/video.html
  • Erik FriesenErik Friesen Posts: 1,071
    edited 2012-06-08 16:57
    One problem with the gears you have posted is that they have no curve to the meshing face. They both need to be convex, unless they are specially designed for some purpose, I suppose. Also, the inner curve probably won't be round as shown, but rather more squarish.

    Google dxf gear calculators.
  • T ChapT Chap Posts: 4,223
    edited 2012-06-08 19:01
    Very grateful to the responses. The drawing I have is not even close, just a starting point trying to figure it out. I will cnc the gears myself with a semi rigid rubber so there is some forgiveness. Phil, I will test that tomorrow, that is really what I have been struggling over. I will study that gear generator tonight as well. Lot's of knowledge on this forum!
  • T ChapT Chap Posts: 4,223
    edited 2012-06-08 19:16
    That gear calculator linked above is amazing.
  • W9GFOW9GFO Posts: 4,010
    edited 2012-06-08 21:23
    An odd number of teeth on one gear will ensure even wear.
  • bsnutbsnut Posts: 521
    edited 2012-06-09 01:32
    One book you may want to get and that I have, is the "Machinists Handbook". It covers how to make different type gears of all sizes. It also covers how they need to be meshed and everything else about gears. This handbook comes in CD or hard or paperback forms.
  • LoopyBytelooseLoopyByteloose Posts: 12,537
    edited 2012-06-09 04:02
    W9GFO wrote: »
    An odd number of teeth on one gear will ensure even wear.

    How profound, and subtle -- makes sense
  • T ChapT Chap Posts: 4,223
    edited 2012-06-09 05:25
    Interesting about the even odd.
  • Heater.Heater. Posts: 21,230
    edited 2012-06-09 05:40
    I don't get it. If I want a 2:1 ratio how is 26T and 13T going to wear differently than 24T and 12T or 28T and 14T?
  • T ChapT Chap Posts: 4,223
    edited 2012-06-09 05:49
    I assumed he meant that even:even insured that the same teeth always contacted the same teeth, but that even:odd would cause the odd gear to shift to different phases of contact, but I didn't test the theory.

    No, this doesn't seem to be the case.

    Perhaps this does not apply to ratios of 2:1, but may in other cases where phase shift could occur, in which the same teeth did not make the same contact each revolution.
  • GadgetmanGadgetman Posts: 2,436
    edited 2012-06-09 05:54
    Possibly...
    But on a 2:1 ratio, that's not going to happen.
  • Heater.Heater. Posts: 21,230
    edited 2012-06-09 06:20
    If I want a 2:1 ratio or some other simple ratio the teeth on the small gear are always going to meet the same teeth on the large gear.
    But what if my design can tolerate a slight error in ratio? Say I build my 2:1 gear box from 41 and 20 tooth gears. Then every tooth on one gear is going to meet every tooth on the other gear at some point and the wear is then evened out.
  • T ChapT Chap Posts: 4,223
    edited 2012-06-09 06:48
    In theory this is true, unless you have a rarer case of a tooth that is irregular, in which case then the wear is worse for all.
  • Phil Pilgrim (PhiPi)Phil Pilgrim (PhiPi) Posts: 23,514
    edited 2012-06-09 08:35
    W9GFO wrote:
    An odd number of teeth on one gear will ensure even wear.
    That's only true if the numbers of teeth on the two gears are relatively prime (i.e. don't share any prime factors). That one gear has an odd number of teeth is therefore a necessary condition for even wear, but not a sufficient one. This automatically rules out gear pairs with integer ratios.

    -Phil
  • LoopyBytelooseLoopyByteloose Posts: 12,537
    edited 2012-06-09 09:27
    So it seems a 2 to 1 gear ratio won't work. I get the idea that the right combination means that the gears keep meeting different opposing faces and that evens the wear over all. Thus Phil's discussion of using the right primes.

    Since the application is likely to be low power, it may not matter much at all. And it is far easier to get what you want by a 2 to 1 ration than something like 13 to 7.
  • T ChapT Chap Posts: 4,223
    edited 2012-06-09 09:45
    A quick test from my newly obtained gear knowledge from the Parallax team has proved successful for the task at hand.
    photo(34).JPG
    640 x 478 - 113K
    photo(33).JPG
    640 x 478 - 102K
  • W9GFOW9GFO Posts: 4,010
    edited 2012-06-09 13:08
    Yeah, well phooey. I was trying to make the point with the least number of words.

    A 12/24 pairing will have the same tooth of the small gear always contacting the same two places on the big gear. A 13/24 pairing will have the tooth of the small gear "walking" its way around all of the teeth of the big gear - I think. I'm sure there's a formula to apply.
  • LoopyBytelooseLoopyByteloose Posts: 12,537
    edited 2012-06-11 09:59
    Phil has a way of being precisely correct. We just don't always understand him at first.

    The concept of 'relatively prime' is new to me (meaning not sharing all the same primes?). Still I am fascinated by this walking one gear around the other as it is new to me. I was aware of planets do this, but hadn't consider it a means to make gears fit better via even wear.
  • T ChapT Chap Posts: 4,223
    edited 2012-06-12 06:34
    On a related topic. If I need a 2:1 ratio, and what seems like the best solution for gear size(outer size) is actually too large on the larger gear to fit some constraints, can I accomplish the same thing as a 15 tooth - 30 tooth by something like 3 gears in a row: 7 tooth - 14 tooth - 21 tooth to accomplish a 2:1 end result? I will test this later on the computer. BTW the direction of the final gear does not matter. I just made up those ratios for 3 gears.

    There are 2 fixed shaft center dims. 2.125". So to use 2:1 from one shaft to the other, the outside diam is approx 3" on the larger gear, which is too large. I need the larger gear <= 2". This makes me think to add a third gear to achieve the goal.
  • Phil Pilgrim (PhiPi)Phil Pilgrim (PhiPi) Posts: 23,514
    edited 2012-06-12 07:49
    The center idler gear will not contribute to the reduction ratio. All it does is transfer power. So the ratio of the outer two gears has to be 2:1. But yes, you can do this to reduce the overall size of the gears. The price is a small loss in efficiency. Also, the outer two gears will now turn the same direction, instead of in opposite directions as they did before.

    -Phil
Sign In or Register to comment.