Gyroscope L3G4200D
Greetings I'm new to the forum. I'mworking on autopilot, and I can not resolve a quaternion matrix does anyone know how to complete these parameters? ..also need to know,if the parameters with which tomultiply the cosine matrix are the integration o fan accelerometer? ..thank you very much.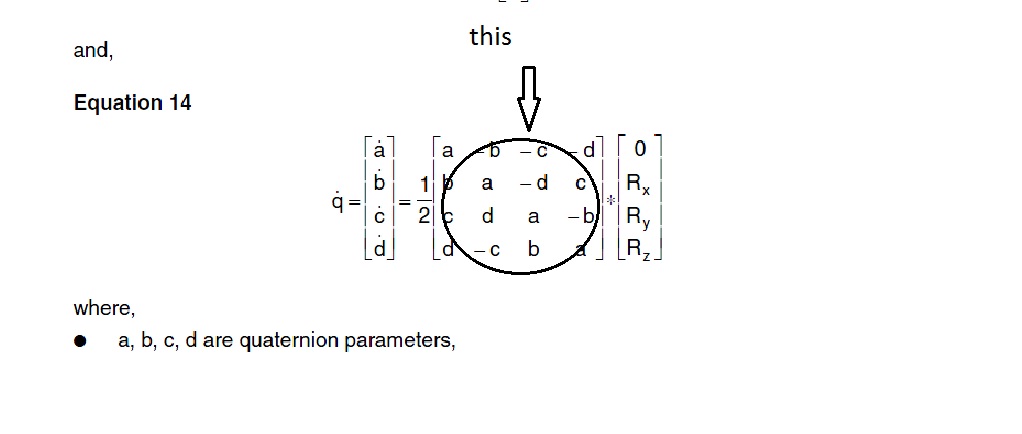




Comments
In any case, your post needs a bit of work. You need to be much more clear on exactly what your question is, preferably with references and enough text to support your question.
http://www.parallax.com/portals/0/downloads/docs/prod/sens/27911-GyroscopeAppNote1.pdf
I'd also like to know where to look to understand the equations on page 37, kaydara just linked to. Does anyone know of a good place to learn about quaternions?
I searched a while ago on the forums for information about quaternions without any luck.
Kaydara, what controller or processor are you using with the L3G4200D?
I think the Propeller should be able to handle the math needed for this task. But as I mentioned above, I haven't found any Propeller software for computing quaternions. I think this would be a very useful feature to add to the Propeller's library of math functions.
I agree
I'm currently working on some code that uses quaternions on the Propeller, although I don't need to do much quaternion specific. The IMU I have produces quaternion output, and the algorithm that I am using uses quaternions natively. Basically all I need to write myself is the multiply and inverse. It's all in assembly.
Note that linux (or at least Ubuntu 11.10) has libcqrlib2 "library for quaternion arithmetic and rotation math".
For understanding quaternions, I found these resources helpful:
http://www.gamedev.net/page/resources/_/technical/math-and-physics/quaternion-powers-r1095
http://www.tobynorris.com/work/prog/csharp/quatview/help/orientations_and_quaternions.htm
www.geometrictools.com/Documentation/Quaternions.pdf
gamma.cs.unc.edu/courses/planning-f07/PAPERS/quaternions.pdf
www.cs.ucr.edu/~vbz/resources/quatut.pdf
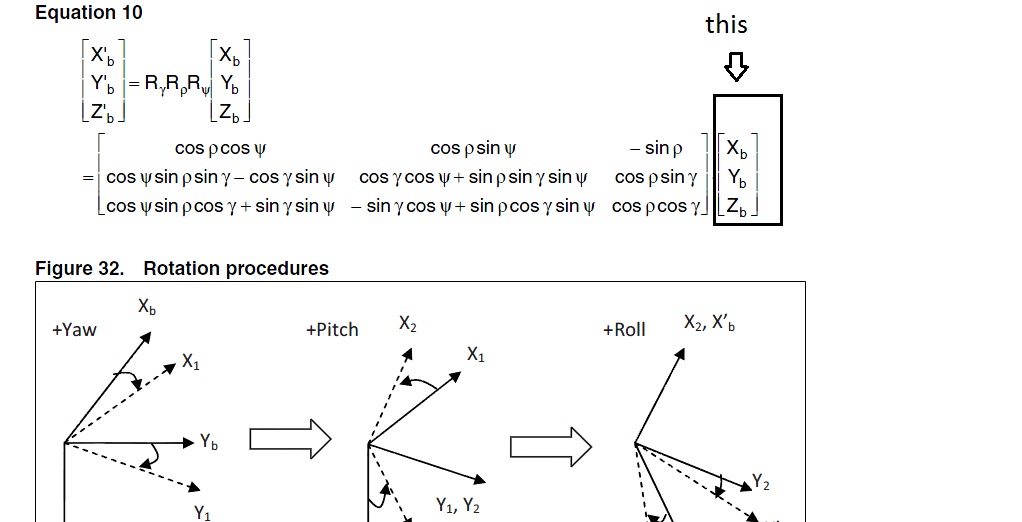
In answer to your original question, x_b, y_b, and z_b is a vector in three dimensional space. The _b subscript denotes that it is in reference to the body, although note that the ' mark nullifies that. Equation 10 is simply rotating the axes through the three angles. (ps: note all the trig functions. yuk!)
In equation 14, a,b,c,d are from the quaternion that represents the starting angle (before the rotation). The equation comes from the derivative of a quaternion, and is how you rotate a quat based on angular rate (not amount). The dot over the q denotes the derivative of the quaternion. Note that in quaternion calculus, the derivative results in another quaternion.
I'm pretty sure I used them in at least one of my math classes, but I've never used them since.
I used to use rotation matrices with computer animation but so far with the Prop, I've only need to rotate one axis at a time (as in a hexapod) and there are usually faster ways to compute angles than using a rotation matrix.
While Equation 10 has a lot of trig functions, the same function is used many times. It wouldn't take as long to calculate as it first appears. (I'm sure you already know this, I just don't want others to be completely scared of a rotation matrix.)
I don't suppose you've posted any of your quaternion code? If not, is it something you'd be willing to do? "No" is a very acceptable answer; I just thought I'd ask.
Thanks again for all the links to quaternion sites and for your explanations.
That's quite a hefty penalty, especially when compared to a quaternion rotation update:
Anyway, I'm still working on the code, and not ready to release it yet. Like the OP I too am working on an autopilot
Matrix refresher: http://www.facstaff.bucknell.edu/mastascu/elessonshtml/Circuit/MatVecMultiply.htm
Here is a little spreadsheet I wrote to calculate the parameters of a control loop for an autopilot: fp speed calculator
I was pleasantly surprised to find the Prop could handle IK calculations for all 18 servos of my hexapod within a servo's 20ms refresh period.
Besides the speed advantage, I understand quaternions aren't susceptible to the same axis cancellation problems that can happen with rotation matrices.
I'm not right ready to work on my autopilot (I wonder if all forum members are secretly working on one), but when I do, I'll need to get these quaternions figured out for myself.
thanks for your answer.then in equation 14. The parameters a-b-c-d, representing the initial angle, do I get data integrating gyroscope or accelerometer?, although logic by integrating the gyroscope data would have to give me certain angles, I'm not sure.
The initial reference is whatever you want it to be. At power up, the system does not know what it's initial orientation is. Usually it doesn't really matter too much if all you want to do is stay level. If you do need your world referenced orientation, you can use your magnemometers to determine yaw (via north), and your accelerometers to determine pitch and roll (via gravity vector). This assumes that you are powering on while stationary.
As a side note, a-b-c-d does not represent the "initial angle" per se, but rather the initial orientation. In any case, I admire you for learning all this in a non-native language.
Integrating the gyros will give you an angle, but it's not reliable over long periods of time. That's why you need some sort of filter to add in the long term stability of other sensors. Typically this is done with either a Kalman Filter (hard) or Direction Cosine Matrix (easier).
thanks SRLM, the truth is there is a forum parallax Spanish, but I have not answered these questions as necessary.