16 bit Calculation help!

ssande · 2012-03-23 09:21

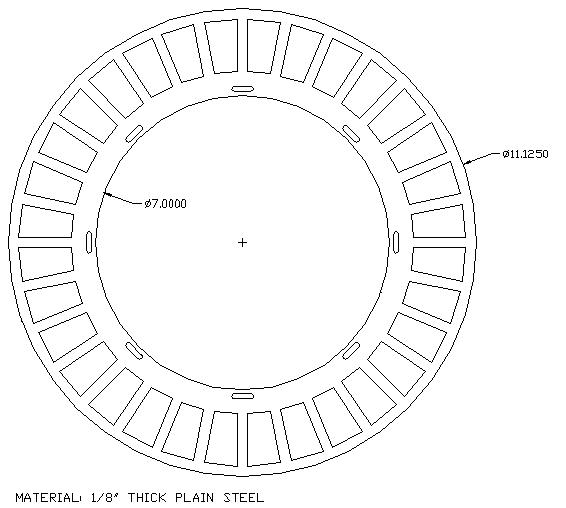
I am trying to calculate an RPM based on Pulsin data from a sensor reading a wheel. The wheel has 32 segements that are 2.728249 degrees wide each (see attached picture). Dividing 360 degrees by 2.728249 I know each sensor reading multiplied by 131.95 will give me the time it take for one complete revolution. I know I am measuring a small portion of a revolution and can live with that precision, but my problem is calculating the rpm within the Basic Stamps 16 bit math. After manipulating the calculation the accuracy is out the door.

The calculation in my spread sheet is:

(1 / (sensor time x (360 / 2.728249)) x 6,000,000 = RPM

Example: A sensor time of 178 gives me 255 RPM (the fastest speed I will need to deal with)

Question is how do I fit this into 16 bit math and still get a reasonably accurate result? I cannot multiply the sensor time by anything as it already approaches the 65,535 time limit. I have tried several different ways and calcualted an RPM result of 271 to 454. Ideas?

Scott

Tracy Allen · 2012-03-23 10:15

Combining the numbers, that is equivalent to 45471 / sensorTime. Your example was sensorTime=178 and 255 RPM, but implied that sensorTime could be much larger when the wheel turns slowly. Are you wanting more precision with fractional RPM, for example, 255.45 RPM?

Martin_H · 2012-03-23 10:16

Tracy beat me to it, but here are my steps:

(1 / (sensor time x (360 / 2.728249)) x 6,000,000 = RPM

6,000,000 / (sensor time x (360 / 2.728249) = RPM

360 / 2.728249 is 131.95.

6,000,000 / (sensor time x 131.95) = RPM

Distribute the / operation and remove parenthesis.

6,000,000 / 131.95 / sensor time = RPM

Simplify

45471 / sensor time = RPM

ssande · 2012-03-23 11:36

Thanks for the responses! I guess I should have paid better attention in Algebra!

Phil Pilgrim (PhiPi) · 2012-03-23 11:59

I would definitely not rely on reading the time-width of a segment to get your speed. Your sensor's threshold may make the segment look wider or narrower than it really is. It's much better to measure from leading edge to leading edge or trailing edge to trailing edge. That should also make the math simpler.

-Phil

ssande · 2012-03-23 12:34

Phil,
I understand what your are saying. I set the sensors I am using up on a height gage and at 1/8" sense distance measured the actual distance the sensor reads as I moved a .500" test bar up and down. I can potentially use that as a calibration factor in my program. I also have a flip-flop circuit so I can try out reading from leading edge to leading edge (that does cut down the minimum RPM sesntivity since I will be at the 65535 limit at a higher speed). The RPM portion in my program is for informational purposes while debugging really. The actual program uses the raw time data from each sensor and compares them, so any sensor threshold may not be a big factor (making an assumption which I will need to verify).

ssande · 2012-03-24 13:48

After looking through my code I found that my percentage calculation has a problem. Basically taking two Pulsin numbers (in my case dealing with valid numbers from 178 to 65,535) and calculating a percentage. I have the following code:

CALC:
LET LEFT_RPM = 45471/LEFT_SENSOR_TIME ' Calculate RPM for Left wheel.
LET RIGHT_RPM = 45471/RIGHT_SENSOR_TIME ' Calculate RPM for Right wheel.

LET TEMP = LEFT_SENSOR_TIME / 10 ' Calculate initial wheel slippage percentage.
LET SLIP_PRECENTAGE = RIGHT_SENSOR_TIME * 10 / TEMP
IF SLIP_PRECENTAGE > 100 THEN AdjustPercentage ' If percent is greater than 100, then take inverse of percent
LET SLIP_PRECENTAGE = 100 - SLIP_PRECENTAGE ' (necessary if LEFT_SENSOR_TIME is greater than RIGHT_SENSOR_TIME).
GOTO DISPLAY

ADJUST_PERCENTAGE:
LET SLIP_PRECENTAGE = 10000 / SLIP_PRECENTAGE ' Performs inverse percentage calculation as required.
LET SLIP_PRECENTAGE = 100 - SLIP_PRECENTAGE
GOTO DISPLAY

This compiles, however they way I am going about these calculations introduces rounding errors since I am dividing one of the numbers by 10.

For instance:
LEFT_SENSOR_TIME = 150
RIGHT_SENSOR_TIME = 178

Yields an actual Slip percentage of: 15.7%
The program calculates: 15%
However, if the Left and right times are swapped because of the rounding I get: 11%

Looking for suggestions to improve the accuracy of these calcualtions. This calculation is critical in my program.

Tracy Allen · 2012-03-24 19:13

Generally for ratio problems of this type on the Stamp, you can have recourse to binary long division. It is not too hard, and it can maintain good precision even when dealing with potentially large inputs. The following is an example. You are also losing precision in the calculation of rpm=45471/time, especially when time becomes large.

[SIZE=1][FONT=courier new]left VAR Word
right VAR Word
n VAR Word
d VAR Word
f VAR Word
percent VAR Word
j VAR nib

demo:
  IF left = right THEN
    percent = 10000      ' 100.00  %,  slip = 10000-percent 
    goto show
  IF left > right THEN   ' this puts the larger of the two numbers in the denominator, so n/d<1
        n = left
        d = right
  ELSE
       n = right
       d = left
  ENDIF
  
  IF d>32767 THEN     ' this is necessary (for the math to work) if the arguments are large
       n = n >> 1
       d = d >> 1
  ENDIF

  GOSUB division
  percent = f ** 10000  ' convert binary ratio to decimal ratio
  DEBUG ?n, ?d, ?f
[/FONT][/SIZE][SIZE=1][FONT=courier new]show:
[/FONT][/SIZE][SIZE=1][FONT=courier new]  DEBUG "percent= ",dec percent/100, ".", dec2 percent


division:               ' enter with n<d, d<32768
     for J=15 to 0               ' 16 bits 
         n = n // D << 1                   ' remainder*2 
         f.bit0(J) = n / d               ' next bit 
     next
     return                ' returns fraction as f/65536 implied[/FONT][/SIZE]

ssande · 2012-03-25 09:05

Tracy, thanks for your reply! Your example looks to be for a BS2 - will it work with a BS1 with the else commands reworked? Also, it uses 7 variables which doesn't leave much for anything else. I'm sure with some creativity I can reuse some of the variables through my program.

Tracy Allen · 2012-03-25 10:41

Sorry, I hadn't picked up on the LET command that is the clue that you are working with a BS1. That is more of a challenge! I'm pretty rusty on BS1 programming. It sounds like your program has other tasks as well.

ELSE can be worked around with a couple of IF and GOTO. The divisor variable in the division algorithm is unchanged, so that could reduce number of variables required. The shift operators << and >> are not available on the BS1, but you can substitute *2 and /2. The division algorithm as stated depends on setting individual bits, which can only be done with variable w0 on the BS1. An alternative there is shift and add. It is going to eat up space in the limited BS1 memory though.

16 bit Calculation help!

Comments