Going through XBee Tutorial

Tymkrs · 2012-02-19 17:32

Hi folks! If anyone reads the tymkrs blog (http://tymkrs.tumblr.com) you'll know I've been going through the xbee tutorial and trying to use it with the propeller. Right now, I'm on Page 59 of it http://www.parallax.com/Portals/0/Downloads/docs/prod/rf/122-32450-XBeeTutorial-v1.0.1.pdf and I think I've set things up properly, but I'm still getting some errors:

Two propeller boes - xbees are fit in the xbee slots. Each of them have the code loaded from Page 59 on their eeproms, and are both connected by USB to the computer. When I test/queried them via X-CTU, I got this:

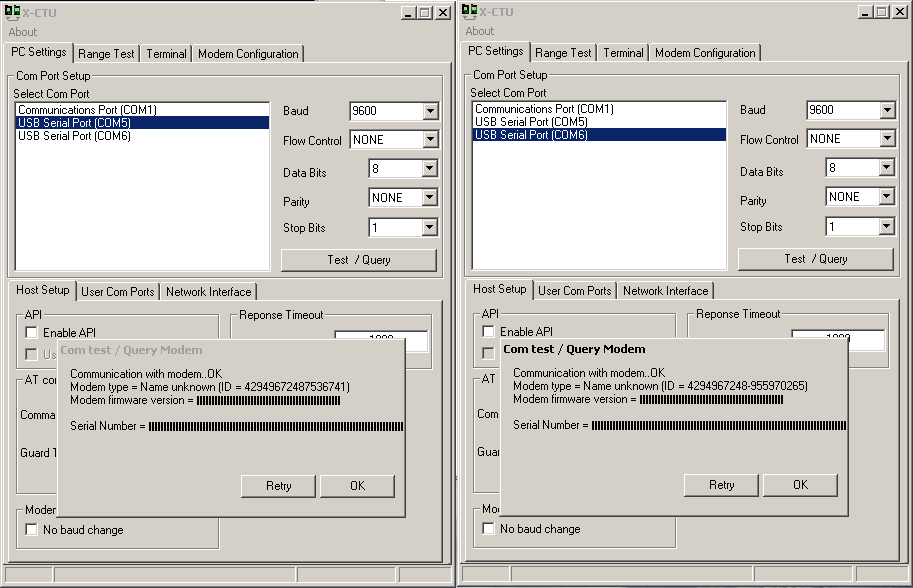
There were some odd blackened squares

Then when I looked at range and terminal:

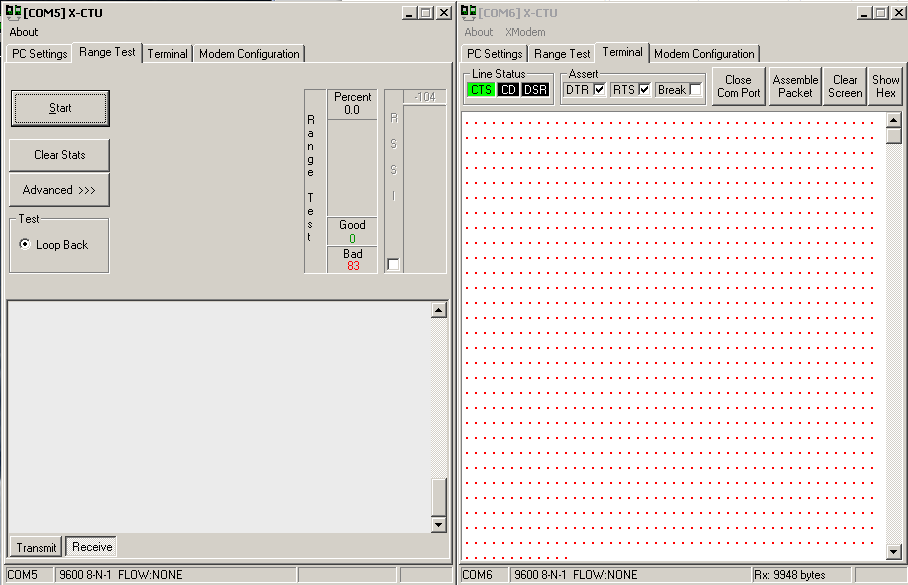
And when I try to go into the modem configuration window, it gives me error messages for both xbees. Anyone have an idea of what's going on?

Thanks!!

Franklin · 2012-02-19 18:01

Have you tried them individually connected to the PC? You might be confusing X-CTU.

Tymkrs · 2012-02-19 18:09

I know they individually work, I was able to go through the earlier parts of the tutorial with no problem. And I might be confusing X-CTU, but I don't see why if the tutorial told me to do it?

Tymkrs · 2012-02-19 18:41

So I just tried: "One XBee on a USB Adapter and one connected to the Propeller running Serial_Pass_Through.spin" - The one connected to the Propeller running Serial_Pass_Through did not work, it had the same issues as shown above, and the one connected to the USB Adapter was okay on its own but unable to talk to the other Xbee.

And now we just tested it on two different computers. So is the tutorial code not right?

Tymkrs · 2012-02-19 18:53

*Cough* Disaster averted, baldness avoided. Whisker told me I was missing some jumper wires (which wasn't stated in the tutorial for noobs such as myself) -_-.

mindrobots · 2012-02-20 08:06

Congrats!!! My experience however from my male patterned perspective is baldness can only be deferred, not avoided.

Martin Hebel · 2012-02-21 05:29

Tymkrs,
Could you explain what you found was wrong? It may have been an oversight in the tutorial and a correction or errata would benefit others. Thanks!

Martin Hebel, author of book.

Tymkrs · 2012-02-22 18:39

Oh it was stupidity on my part Martin

I had the xbee plugged into the xbee port on the propeller BOE, and forgot that I needed to have actual jumper wires between DOUT and DIN and pin 0 and pin 1. I thought it'd be magically connected through some traces that I couldn't see. Whisker found that error out pretty easily. So here's what I just had to do:

By the way - the tutorial is /wonderful/ - I'm currently going through page by page and blogging about it in a super long series on the blog as well as in video. It's almost XBee and Propeller month over here at Tymkrs

http://tymkrs.tumblr.com/

Videos: We're currently uploading the second part showing some xbee configuration but here's the first part:

Martin Hebel · 2012-02-23 05:06

ok

Thanks for letting me know. Great video and blog! I'm glad you are enjoying the tutorial.

-Martin

Tymkrs · 2012-02-29 03:28

Still going through the code and now looking at some code analysis for a remote xbee node.

I'm looking at the ctra stuff and wanted to clarify if this "interpretation" was correct:

Assuming frqa := 1 and phsa := 0 in counter A, Counter A will, on every clock cycle, bump phsa up by 1 because frqa := 1. If frqa was := 2, then phsa would go up by 2 every clock cycle?

The mode is %00100 which can be a numerically controlled oscillator (NCO) which works on PHSx[31]. Does this mean that phsx is working on pin 31?

The following was read in a PDF on ctrs for dummies

and I wanted to check something:

"There are some operating modes that associate the most significant bit of PHSx, PHSx[31] with an output pin, the pin goes high every time a 1 appears in PHSx[31], how often that happens depends on the value in FRQx and because of that it is described in the manual as a numerically controlled oscillator or NCO"

So whenever FRQx calls for an increment (let's say FRQx := 1), then each clock cycle PHSx[31] would toggle pin 31? If so, then does the pin mirror what pin 31 is doing?

Many thanks for any answers I could get

I'm sure I'm making this more complicated than it needs to be!

Tymkrs · 2012-03-01 15:17

So update to my code analysis stuff:

Q: "Assuming frqa := 1 and phsa := 0 in counter A, Counter A will, on every clock cycle, bump phsa up by 1 because frqa := 1. If frqa was := 2, then phsa would go up by 2 every clock cycle?"

A: Yes, this is essentially how it works.

Haven't found an answer to the phsx[31] thing yet, but in continuing on with the questions, I'm looking at this portion:

I know it's supposed to be an "optimized" way to solve: "Result = freq * (2^32) / clkfreq"

But I can't see how getting the difference between freq and clkfreq and incrementing/bitshifting Result and Freq leads to that? Anyone willing to give an example?

Many thanks - Addie

Martin Hebel · 2012-03-01 21:01

Hi,
If that's from my code, it's probably from an example from code by Andy Lindsay I borrowed, and I believe it it was a trick Chip Gracey showed him. Which means it is not meant for mere mortals such as ourselves to understand!

But seriously (kinda), it is code I borrrowed and never fully grocked in fullness. Maybe another guru can help out, but like many programmers, we find cool code that does the trick and use it. The propeller counters make my head hurt.

Tymkrs · 2012-03-02 17:56

It is quite elegantly written out as you have said Martin! But I managed to get a rudimentary understanding of this portion of the code. This is mostly binary math and awesome bitshifting. The code is supposed to do this equation: Result = freq * 2^32 / clkfreq.

If we look at the code, we see a lot of comparison and a lot of subtraction. But let's think about this in terms of long division. When you divide a number, you compare to see if that divisor can "fit into" the dividend. If you can't fit it in, you add zeros (or in this code's case, you bitshift to the left). Then you subtract the divisor (clkfreq) from that number.

So in this code we see whether freq is equal to or greater than clkfreq. If it is, we subtract and repeat the process. But in the code you also see that we multiply freq by 2^32. Well each time we bitshift, that's like x * 2, and if we repeat this code 33 times, you pretty much get your freq * 2^32. And with the subtraction, you divide by clkfreq!

I have a post on the tymkrs forums that has a few more details and a code example from our friend @feltonchris for anyone interested: http://www.tymkrs.com/forum/viewtopic.php?pid=829#p829

And I'll have a post coming up that goes through bitshifting and the binary math involved in this step by step.

Tracy Allen · 2012-03-03 13:20

Right, it is integer binary long division. It has applications beyond calculating freq values for the counter. (I use essentially the same algorithm on the 16 bit BASIC Stamp for problems involving calibration of sensors.) Here it is in a more general form in Spin for the Prop, where it is dividing numerator y by denominator x and returning a result to a certain number of bits.

PUB binFrac (y, x, nbits) : f                                         ' calculate f = y/x * 2^b
' nbits is number of bits
' y is numerator, x is denominator

' enter with {x > y, x < 2^30, y <= 2^30}
' exit with f: f/(2^b) =<  y/x =< (f+1) / (2^b)
' that is, f / 2^b is the closest approximation to the original fraction for that b.
 ' 
  repeat nbits                      
    y <<= 1
    f <<= 1
    if y => x    '  
      y -= x
      f++

I think it helps if you think of the result as an approximation to the original fraction. That is, each step in the algorithm gives better approximation with a binary denominator that increase in precision by powers of two.

Take as an example your frqa calculation. The denominator is the Prop clock frequency, let it be clkfreq = 80_000_000, and the numerator is say 10_000 Hz. When you work out 10_000/80_000_000 on a calculator it comes out to the decimal fraction 0.000125. And multiplied times 2^32 that is 536870.912, but drop he remainder and just call it 536870.

I like to think of that as 536870/2^32. It is the closest approximation to 10_000/80_000_000 that has 2^32 as denominator:
10_000/80_000_000 = 536870/2^32.
Exact value 0.000125, approximation 0.0001249997877.
Think of it also as a binary fraction with a binary radix point on the left of the 32-bit field:
0.0000_0000_0000_1000_0011_0001_0010_0110
Muliply that times 2^32 is the same as shifting the radix point 32 places to the right, so you have
1000_0011_0001_0010_0110
which of course equals 536870 in decimal.

Here is how the calculation proceeds step by step:

The first step is comparing the value to 1/2 and finding it to be less, and so it goes until the 13th step. There it finds that 100000/80000000 is greater than 1/8192, so it accumulates a 1. It continues shifting, but it has to get up to the 19th and 20th bit before it accumulates more 1s. If you were to stop with 20 bits, you would have (131 / 2^20 = 0.000124931) as the closest approximation to 10000000/80000000 with 20 bits in the denominator. Out to 32 steps and it is the fraction we have been talking about, the one that has to go into frqa for the NCO mode of the counter.

In the counter, think how many times you have to add 536870 to the 32 bit accumulator before it overflows. Viol

Tymkrs · 2012-03-03 22:55

Hey Tracy,

I actually was able to go step by step through it for the post which will show up in a couple of weeks on our tumblr, but this is /great/ that there's another example with different values! I'll be sure to include this example in the post and thanks so much for taking the time to make this example!

Tymkrs · 2012-03-04 17:48

Tymkrs wrote: »

The mode is 100 which can be a numerically controlled oscillator (NCO) which works on PHSx[31]. Does this mean that phsx is working on pin 31?

So I found the noob answer to this (written in the blog soon): So binary bits are numbered 0 to 31, though at bit number 31, the total binary value is 2^32. Once the binary value reaches 2^32, it will wrap and go back to 0. The value at that point will equal 2^31 + 2^30 + 2^29...and all of that will equal 2^32. PHSx[31] says essentially that if bit 31 is on, then PINA will be on, and if bit 31 is off, PINA will be off.

PHSx-Carry means that when the carry actually happens (from whatever large value to 0), PINA turns on. PINA is determined by bytes 0..5 in the CTRA register. Then it turns off the next time PHSx gets something added to it unless that something causes it to carry again.

Going through XBee Tutorial

Comments