FIR2PASM: Automatic FIR Filter Code Generator
 Phil Pilgrim (PhiPi)
Posts: 23,514
Phil Pilgrim (PhiPi)
Posts: 23,514
[size=+1]Introduction[/size]
I've posted an online service that converts FIR filter parameters to PASM code that can be used for real-time audio filtering. You can access it here:
You will have to obtain the filter coefficients from a filter design program, such as these online versions:
or this freeware Windows program:
Once the filter has been designed using one of these programs, just copy the filter coefficients into the box. Some such filters have non-unity gain, so be sure to enter the filter gain in the box provided. If you want non-unity gain, enter that, too.
The "bits of precision" choice will impact both the accuracy of the filter and its execution time. Twelve bits seems to work for out-of-band suppression to -40 dB. Getting to -60 dB has proven to be difficult at any level of precision, but you can try. A lot also depends on the resolution of the signal feeding the filter. In the filter test program attached below, the signals feeding it are in the -10000 to +10000 range (~14 bits).
The resulting Propeller object will list the number of instructions in each iteration of the filter (not including input and output), so you can determine whether it will meet your sampling rate requirements. You do not need to use the resultant code in its object form, BTW; you can also just cut and paste the PASM into your own signal-processing program.
[size=+1]Brief Tutorial[/size]
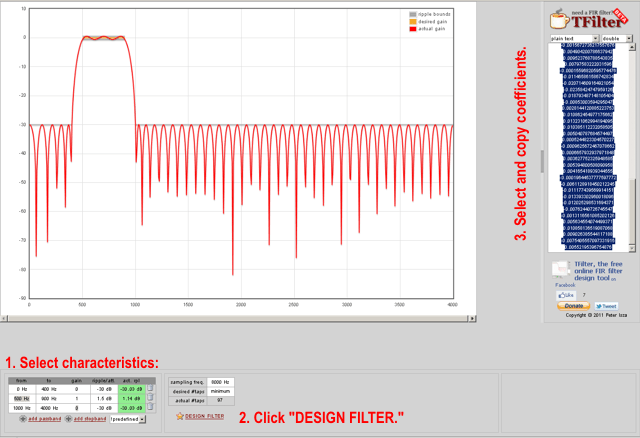
Here is a step-by-step example using the TFilter online filter designer. We will be designing a filter with a passband between 500 Hz and 900 Hz, out-of-band response no more than -30 dB, assuming an 8000 Hz sampling rate. Here's the TFilter screen:

Next, we paste the coefficients into the FIR2PASM window, and select the default 12-bit precision and unity gain:

After clicking Submit, we have a choice of opening the resulting object in the Propeller Tool or saving it. Let's save it to our projects directory:

Then we can open it in the Propeller Tool:
Here, we see that the filter loop uses 312 instructions, exclusive of sample load and result store operations. With an 80 MHz clock, that would amount to 15.6 µs to process each sample, giving us a ceiling of 64K samples per second -- well within the design specs of 8000 samples per second.
We can run this object using the attached test program. (Note: FIR2PASM does not check to see if the PASM program fits in its cog. Some PASM programs may be too large. If that's the case, try reducing the precision or relaxing the filter requirements.)
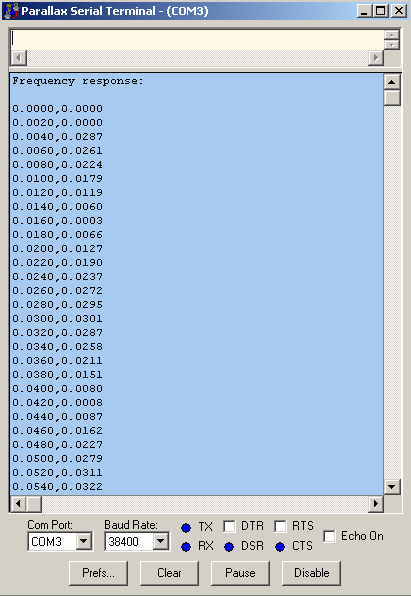
Next, we can select and copy all 501 lines of numerical output from the PST window:

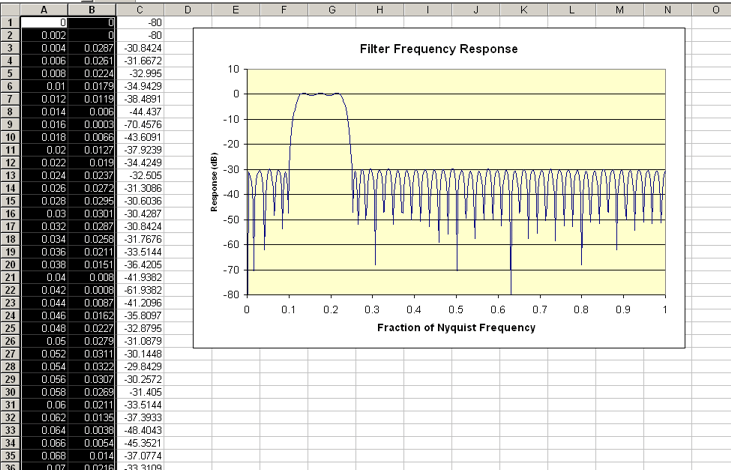
and paste it into the included Excel spreadsheet (fir_response.xls):

This gives us a chance to compare the actual frequency response with the one displayed by TFilter.
Enjoy!
-Phil
I've posted an online service that converts FIR filter parameters to PASM code that can be used for real-time audio filtering. You can access it here:
You will have to obtain the filter coefficients from a filter design program, such as these online versions:
or this freeware Windows program:
Once the filter has been designed using one of these programs, just copy the filter coefficients into the box. Some such filters have non-unity gain, so be sure to enter the filter gain in the box provided. If you want non-unity gain, enter that, too.
The "bits of precision" choice will impact both the accuracy of the filter and its execution time. Twelve bits seems to work for out-of-band suppression to -40 dB. Getting to -60 dB has proven to be difficult at any level of precision, but you can try. A lot also depends on the resolution of the signal feeding the filter. In the filter test program attached below, the signals feeding it are in the -10000 to +10000 range (~14 bits).
The resulting Propeller object will list the number of instructions in each iteration of the filter (not including input and output), so you can determine whether it will meet your sampling rate requirements. You do not need to use the resultant code in its object form, BTW; you can also just cut and paste the PASM into your own signal-processing program.
[size=+1]Brief Tutorial[/size]
Here is a step-by-step example using the TFilter online filter designer. We will be designing a filter with a passband between 500 Hz and 900 Hz, out-of-band response no more than -30 dB, assuming an 8000 Hz sampling rate. Here's the TFilter screen:
Next, we paste the coefficients into the FIR2PASM window, and select the default 12-bit precision and unity gain:
After clicking Submit, we have a choice of opening the resulting object in the Propeller Tool or saving it. Let's save it to our projects directory:
Then we can open it in the Propeller Tool:
{{{
*****************************************
* FIR Filter Propeller Object *
* generated by www.phipi.com/fir2pasm *
* from the parameters given in the DAT *
* section of this file. *
*****************************************
Created: Wed Jul 20 22:55:47 2011 UTC
}}
CON
SIZE = 97
BITS = 12
VAR
long busy, value
PUB start
'' Start the FIR filter cog.
cognew(@fir_filter, @busy)
PUB filter(yy)
'' Return the current FIR-filtered value of sample yy in data stream.
value := yy
busy~~
repeat while busy
return value
DAT
'==========================================================================
'Parameters Given
'
' 97 coefficients:
'
' +5.52195397e-03
' -7.54055571e-03
' +9.02638554e-03
' +1.08581365e-02
' +5.63455407e-03
' -1.31165611e-03
' -7.62440727e-03
' -1.20252985e-02
' -1.33933030e-02
' -1.11774396e-02
' -6.11289185e-03
' -1.96445378e-04
' +4.16541894e-03
' +5.39480051e-03
' +3.62775233e-03
' +6.65793294e-04
' -9.62567247e-04
' +5.24482330e-04
' +5.04078768e-03
' +1.03851122e-02
' +1.32310630e-02
' +1.08624550e-02
' +2.81441209e-03
' -8.53003594e-03
' -1.87934871e-02
' -2.35842475e-02
' -2.07146092e-02
' -1.14658616e-02
' -1.55968206e-04
' +7.97583222e-03
' +9.52376879e-03
' +4.90420079e-03
' -1.56727362e-03
' -3.77260158e-03
' +2.78440579e-03
' +1.78837993e-02
' +3.56251650e-02
' +4.63757046e-02
' +4.10435277e-02
' +1.59326095e-02
' -2.42371919e-02
' -6.67431937e-02
' -9.52687093e-02
' -9.62452428e-02
' -6.51217233e-02
' -9.13807555e-03
' +5.43968086e-02
' +1.04211063e-01
' +1.23032257e-01
' +1.04211063e-01
' +5.43968086e-02
' -9.13807555e-03
' -6.51217233e-02
' -9.62452428e-02
' -9.52687093e-02
' -6.67431937e-02
' -2.42371919e-02
' +1.59326095e-02
' +4.10435277e-02
' +4.63757046e-02
' +3.56251650e-02
' +1.78837993e-02
' +2.78440579e-03
' -3.77260158e-03
' -1.56727362e-03
' +4.90420079e-03
' +9.52376879e-03
' +7.97583222e-03
' -1.55968206e-04
' -1.14658616e-02
' -2.07146092e-02
' -2.35842475e-02
' -1.87934871e-02
' -8.53003594e-03
' +2.81441209e-03
' +1.08624550e-02
' +1.32310630e-02
' +1.03851122e-02
' +5.04078768e-03
' +5.24482330e-04
' -9.62567247e-04
' +6.65793294e-04
' +3.62775233e-03
' +5.39480051e-03
' +4.16541894e-03
' -1.96445378e-04
' -6.11289185e-03
' -1.11774396e-02
' -1.33933030e-02
' -1.20252985e-02
' -7.62440727e-03
' -1.31165611e-03
' +5.63455407e-03
' +1.08581365e-02
' +9.02638554e-03
' -7.54055571e-03
' +5.52195397e-03
'
' Stated gain: 1.0000000
' Desired gain: 1.0000000
' Precision: 12 bits.
'
'Resulting PASM instructions in loop: 312
'==========================================================================
org 0
fir_filter mov arg_addr,par 'Initialize the hub address for the data exchange.
add arg_addr,#4
'Further user initialization code can be added here.
main_lp 'DO NOT MODIFY.
'The next line can be altered to acquire the next input sample in another way.
call #get_x 'Read the next input.
'Compute input * filter coefficients.
mov h+34,x 'DO NOT MODIFY.
mov h+35,x 'DO NOT MODIFY.
mov h+40,x 'DO NOT MODIFY.
mov h+39,x 'DO NOT MODIFY.
sar x,#1 'DO NOT MODIFY.
mov h+38,x 'DO NOT MODIFY.
mov h+33,x 'DO NOT MODIFY.
mov h+36,x 'DO NOT MODIFY.
mov h+29,x 'DO NOT MODIFY.
sar x,#1 'DO NOT MODIFY.
mov h+30,x 'DO NOT MODIFY.
sub h+34,x 'DO NOT MODIFY.
mov h+32,x 'DO NOT MODIFY.
sub h+35,x 'DO NOT MODIFY.
mov h+20,x 'DO NOT MODIFY.
sub h+39,x 'DO NOT MODIFY.
mov h+28,x 'DO NOT MODIFY.
sar x,#1 'DO NOT MODIFY.
mov h+22,x 'DO NOT MODIFY.
mov h+21,x 'DO NOT MODIFY.
mov h+9,x 'DO NOT MODIFY.
mov h+27,x 'DO NOT MODIFY.
mov h+8,x 'DO NOT MODIFY.
mov h+3,x 'DO NOT MODIFY.
sub h+29,x 'DO NOT MODIFY.
mov h+7,x 'DO NOT MODIFY.
mov h+19,x 'DO NOT MODIFY.
mov h+31,x 'DO NOT MODIFY.
sar x,#1 'DO NOT MODIFY.
add h+30,x 'DO NOT MODIFY.
sub h+32,x 'DO NOT MODIFY.
mov h+23,x 'DO NOT MODIFY.
mov h+37,x 'DO NOT MODIFY.
mov h+1,x 'DO NOT MODIFY.
mov h+6,x 'DO NOT MODIFY.
sub h+20,x 'DO NOT MODIFY.
add h+39,x 'DO NOT MODIFY.
mov h+10,x 'DO NOT MODIFY.
mov h+0,x 'DO NOT MODIFY.
sub h+38,x 'DO NOT MODIFY.
mov h+24,x 'DO NOT MODIFY.
mov h+2,x 'DO NOT MODIFY.
mov h+16,x 'DO NOT MODIFY.
mov h+4,x 'DO NOT MODIFY.
mov h+18,x 'DO NOT MODIFY.
sar x,#1 'DO NOT MODIFY.
sub h+22,x 'DO NOT MODIFY.
add h+21,x 'DO NOT MODIFY.
mov h+11,x 'DO NOT MODIFY.
mov h+17,x 'DO NOT MODIFY.
sub h+9,x 'DO NOT MODIFY.
add h+33,x 'DO NOT MODIFY.
sub h+3,x 'DO NOT MODIFY.
mov h+12,x 'DO NOT MODIFY.
sub h+7,x 'DO NOT MODIFY.
add h+28,x 'DO NOT MODIFY.
mov h+15,x 'DO NOT MODIFY.
mov h+26,x 'DO NOT MODIFY.
add h+19,x 'DO NOT MODIFY.
sar x,#1 'DO NOT MODIFY.
add h+30,x 'DO NOT MODIFY.
add h+34,x 'DO NOT MODIFY.
add h+35,x 'DO NOT MODIFY.
sub h+40,x 'DO NOT MODIFY.
add h+39,x 'DO NOT MODIFY.
mov h+25,x 'DO NOT MODIFY.
sub h+10,x 'DO NOT MODIFY.
sub h+0,x 'DO NOT MODIFY.
add h+27,x 'DO NOT MODIFY.
sub h+8,x 'DO NOT MODIFY.
add h+24,x 'DO NOT MODIFY.
add h+36,x 'DO NOT MODIFY.
add h+16,x 'DO NOT MODIFY.
sub h+4,x 'DO NOT MODIFY.
sar x,#1 'DO NOT MODIFY.
mov h+14,x 'DO NOT MODIFY.
add h+32,x 'DO NOT MODIFY.
add h+37,x 'DO NOT MODIFY.
add h+21,x 'DO NOT MODIFY.
sub h+17,x 'DO NOT MODIFY.
sub h+9,x 'DO NOT MODIFY.
sub h+3,x 'DO NOT MODIFY.
mov h+5,x 'DO NOT MODIFY.
sub h+29,x 'DO NOT MODIFY.
add h+2,x 'DO NOT MODIFY.
add h+15,x 'DO NOT MODIFY.
sub h+19,x 'DO NOT MODIFY.
sar x,#1 'DO NOT MODIFY.
sub h+22,x 'DO NOT MODIFY.
sub h+34,x 'DO NOT MODIFY.
add h+35,x 'DO NOT MODIFY.
sub h+1,x 'DO NOT MODIFY.
add h+39,x 'DO NOT MODIFY.
sub h+25,x 'DO NOT MODIFY.
sub h+0,x 'DO NOT MODIFY.
sub h+38,x 'DO NOT MODIFY.
sub h+8,x 'DO NOT MODIFY.
add h+36,x 'DO NOT MODIFY.
mov h+13,x 'DO NOT MODIFY.
sub h+12,x 'DO NOT MODIFY.
add h+16,x 'DO NOT MODIFY.
add h+18,x 'DO NOT MODIFY.
sar x,#1 'DO NOT MODIFY.
sub h+14,x 'DO NOT MODIFY.
sub h+32,x 'DO NOT MODIFY.
add h+37,x 'DO NOT MODIFY.
sub h+40,x 'DO NOT MODIFY.
sub h+6,x 'DO NOT MODIFY.
add h+11,x 'DO NOT MODIFY.
sub h+17,x 'DO NOT MODIFY.
add h+10,x 'DO NOT MODIFY.
add h+9,x 'DO NOT MODIFY.
add h+27,x 'DO NOT MODIFY.
add h+33,x 'DO NOT MODIFY.
sub h+24,x 'DO NOT MODIFY.
add h+5,x 'DO NOT MODIFY.
add h+29,x 'DO NOT MODIFY.
add h+7,x 'DO NOT MODIFY.
add h+28,x 'DO NOT MODIFY.
sub h+4,x 'DO NOT MODIFY.
sub h+26,x 'DO NOT MODIFY.
add h+31,x 'DO NOT MODIFY.
'Apply input * coefficients to FIR stages and shift one step.
add stage+0,h+0 'DO NOT MODIFY.
mov y,stage+0 'DO NOT MODIFY.
sar y,#3 'DO NOT MODIFY.
'Writing the y value here allows overlapped processing with another cog.
'Delete the next line to process the output further in this cog.
call #put_y 'Write the next output.
sub stage+1,h+1 'DO NOT MODIFY.
mov stage+0,stage+1 'DO NOT MODIFY.
add stage+2,h+2 'DO NOT MODIFY.
mov stage+1,stage+2 'DO NOT MODIFY.
add stage+3,h+3 'DO NOT MODIFY.
mov stage+2,stage+3 'DO NOT MODIFY.
add stage+4,h+4 'DO NOT MODIFY.
mov stage+3,stage+4 'DO NOT MODIFY.
sub stage+5,h+5 'DO NOT MODIFY.
mov stage+4,stage+5 'DO NOT MODIFY.
sub stage+6,h+6 'DO NOT MODIFY.
mov stage+5,stage+6 'DO NOT MODIFY.
sub stage+7,h+7 'DO NOT MODIFY.
mov stage+6,stage+7 'DO NOT MODIFY.
sub stage+8,h+8 'DO NOT MODIFY.
mov stage+7,stage+8 'DO NOT MODIFY.
sub stage+9,h+9 'DO NOT MODIFY.
mov stage+8,stage+9 'DO NOT MODIFY.
sub stage+10,h+10 'DO NOT MODIFY.
mov stage+9,stage+10 'DO NOT MODIFY.
mov stage+10,stage+11 'DO NOT MODIFY.
add stage+12,h+11 'DO NOT MODIFY.
mov stage+11,stage+12 'DO NOT MODIFY.
add stage+13,h+0 'DO NOT MODIFY.
mov stage+12,stage+13 'DO NOT MODIFY.
add stage+14,h+12 'DO NOT MODIFY.
mov stage+13,stage+14 'DO NOT MODIFY.
add stage+15,h+13 'DO NOT MODIFY.
mov stage+14,stage+15 'DO NOT MODIFY.
sub stage+16,h+14 'DO NOT MODIFY.
mov stage+15,stage+16 'DO NOT MODIFY.
add stage+17,h+13 'DO NOT MODIFY.
mov stage+16,stage+17 'DO NOT MODIFY.
add stage+18,h+15 'DO NOT MODIFY.
mov stage+17,stage+18 'DO NOT MODIFY.
add stage+19,h+16 'DO NOT MODIFY.
mov stage+18,stage+19 'DO NOT MODIFY.
add stage+20,h+8 'DO NOT MODIFY.
mov stage+19,stage+20 'DO NOT MODIFY.
add stage+21,h+3 'DO NOT MODIFY.
mov stage+20,stage+21 'DO NOT MODIFY.
add stage+22,h+17 'DO NOT MODIFY.
mov stage+21,stage+22 'DO NOT MODIFY.
sub stage+23,h+18 'DO NOT MODIFY.
mov stage+22,stage+23 'DO NOT MODIFY.
sub stage+24,h+19 'DO NOT MODIFY.
mov stage+23,stage+24 'DO NOT MODIFY.
sub stage+25,h+20 'DO NOT MODIFY.
mov stage+24,stage+25 'DO NOT MODIFY.
sub stage+26,h+21 'DO NOT MODIFY.
mov stage+25,stage+26 'DO NOT MODIFY.
sub stage+27,h+22 'DO NOT MODIFY.
mov stage+26,stage+27 'DO NOT MODIFY.
mov stage+27,stage+28 'DO NOT MODIFY.
add stage+29,h+23 'DO NOT MODIFY.
mov stage+28,stage+29 'DO NOT MODIFY.
add stage+30,h+24 'DO NOT MODIFY.
mov stage+29,stage+30 'DO NOT MODIFY.
add stage+31,h+15 'DO NOT MODIFY.
mov stage+30,stage+31 'DO NOT MODIFY.
sub stage+32,h+25 'DO NOT MODIFY.
mov stage+31,stage+32 'DO NOT MODIFY.
sub stage+33,h+26 'DO NOT MODIFY.
mov stage+32,stage+33 'DO NOT MODIFY.
add stage+34,h+17 'DO NOT MODIFY.
mov stage+33,stage+34 'DO NOT MODIFY.
add stage+35,h+27 'DO NOT MODIFY.
mov stage+34,stage+35 'DO NOT MODIFY.
add stage+36,h+28 'DO NOT MODIFY.
mov stage+35,stage+36 'DO NOT MODIFY.
add stage+37,h+29 'DO NOT MODIFY.
mov stage+36,stage+37 'DO NOT MODIFY.
add stage+38,h+30 'DO NOT MODIFY.
mov stage+37,stage+38 'DO NOT MODIFY.
add stage+39,h+31 'DO NOT MODIFY.
mov stage+38,stage+39 'DO NOT MODIFY.
sub stage+40,h+32 'DO NOT MODIFY.
mov stage+39,stage+40 'DO NOT MODIFY.
sub stage+41,h+33 'DO NOT MODIFY.
mov stage+40,stage+41 'DO NOT MODIFY.
sub stage+42,h+34 'DO NOT MODIFY.
mov stage+41,stage+42 'DO NOT MODIFY.
sub stage+43,h+35 'DO NOT MODIFY.
mov stage+42,stage+43 'DO NOT MODIFY.
sub stage+44,h+36 'DO NOT MODIFY.
mov stage+43,stage+44 'DO NOT MODIFY.
sub stage+45,h+37 'DO NOT MODIFY.
mov stage+44,stage+45 'DO NOT MODIFY.
add stage+46,h+38 'DO NOT MODIFY.
mov stage+45,stage+46 'DO NOT MODIFY.
add stage+47,h+39 'DO NOT MODIFY.
mov stage+46,stage+47 'DO NOT MODIFY.
add stage+48,h+40 'DO NOT MODIFY.
mov stage+47,stage+48 'DO NOT MODIFY.
add stage+49,h+39 'DO NOT MODIFY.
mov stage+48,stage+49 'DO NOT MODIFY.
add stage+50,h+38 'DO NOT MODIFY.
mov stage+49,stage+50 'DO NOT MODIFY.
sub stage+51,h+37 'DO NOT MODIFY.
mov stage+50,stage+51 'DO NOT MODIFY.
sub stage+52,h+36 'DO NOT MODIFY.
mov stage+51,stage+52 'DO NOT MODIFY.
sub stage+53,h+35 'DO NOT MODIFY.
mov stage+52,stage+53 'DO NOT MODIFY.
sub stage+54,h+34 'DO NOT MODIFY.
mov stage+53,stage+54 'DO NOT MODIFY.
sub stage+55,h+33 'DO NOT MODIFY.
mov stage+54,stage+55 'DO NOT MODIFY.
sub stage+56,h+32 'DO NOT MODIFY.
mov stage+55,stage+56 'DO NOT MODIFY.
add stage+57,h+31 'DO NOT MODIFY.
mov stage+56,stage+57 'DO NOT MODIFY.
add stage+58,h+30 'DO NOT MODIFY.
mov stage+57,stage+58 'DO NOT MODIFY.
add stage+59,h+29 'DO NOT MODIFY.
mov stage+58,stage+59 'DO NOT MODIFY.
add stage+60,h+28 'DO NOT MODIFY.
mov stage+59,stage+60 'DO NOT MODIFY.
add stage+61,h+27 'DO NOT MODIFY.
mov stage+60,stage+61 'DO NOT MODIFY.
add stage+62,h+17 'DO NOT MODIFY.
mov stage+61,stage+62 'DO NOT MODIFY.
sub stage+63,h+26 'DO NOT MODIFY.
mov stage+62,stage+63 'DO NOT MODIFY.
sub stage+64,h+25 'DO NOT MODIFY.
mov stage+63,stage+64 'DO NOT MODIFY.
add stage+65,h+15 'DO NOT MODIFY.
mov stage+64,stage+65 'DO NOT MODIFY.
add stage+66,h+24 'DO NOT MODIFY.
mov stage+65,stage+66 'DO NOT MODIFY.
add stage+67,h+23 'DO NOT MODIFY.
mov stage+66,stage+67 'DO NOT MODIFY.
mov stage+67,stage+68 'DO NOT MODIFY.
sub stage+69,h+22 'DO NOT MODIFY.
mov stage+68,stage+69 'DO NOT MODIFY.
sub stage+70,h+21 'DO NOT MODIFY.
mov stage+69,stage+70 'DO NOT MODIFY.
sub stage+71,h+20 'DO NOT MODIFY.
mov stage+70,stage+71 'DO NOT MODIFY.
sub stage+72,h+19 'DO NOT MODIFY.
mov stage+71,stage+72 'DO NOT MODIFY.
sub stage+73,h+18 'DO NOT MODIFY.
mov stage+72,stage+73 'DO NOT MODIFY.
add stage+74,h+17 'DO NOT MODIFY.
mov stage+73,stage+74 'DO NOT MODIFY.
add stage+75,h+3 'DO NOT MODIFY.
mov stage+74,stage+75 'DO NOT MODIFY.
add stage+76,h+8 'DO NOT MODIFY.
mov stage+75,stage+76 'DO NOT MODIFY.
add stage+77,h+16 'DO NOT MODIFY.
mov stage+76,stage+77 'DO NOT MODIFY.
add stage+78,h+15 'DO NOT MODIFY.
mov stage+77,stage+78 'DO NOT MODIFY.
add stage+79,h+13 'DO NOT MODIFY.
mov stage+78,stage+79 'DO NOT MODIFY.
sub stage+80,h+14 'DO NOT MODIFY.
mov stage+79,stage+80 'DO NOT MODIFY.
add stage+81,h+13 'DO NOT MODIFY.
mov stage+80,stage+81 'DO NOT MODIFY.
add stage+82,h+12 'DO NOT MODIFY.
mov stage+81,stage+82 'DO NOT MODIFY.
add stage+83,h+0 'DO NOT MODIFY.
mov stage+82,stage+83 'DO NOT MODIFY.
add stage+84,h+11 'DO NOT MODIFY.
mov stage+83,stage+84 'DO NOT MODIFY.
mov stage+84,stage+85 'DO NOT MODIFY.
sub stage+86,h+10 'DO NOT MODIFY.
mov stage+85,stage+86 'DO NOT MODIFY.
sub stage+87,h+9 'DO NOT MODIFY.
mov stage+86,stage+87 'DO NOT MODIFY.
sub stage+88,h+8 'DO NOT MODIFY.
mov stage+87,stage+88 'DO NOT MODIFY.
sub stage+89,h+7 'DO NOT MODIFY.
mov stage+88,stage+89 'DO NOT MODIFY.
sub stage+90,h+6 'DO NOT MODIFY.
mov stage+89,stage+90 'DO NOT MODIFY.
sub stage+91,h+5 'DO NOT MODIFY.
mov stage+90,stage+91 'DO NOT MODIFY.
add stage+92,h+4 'DO NOT MODIFY.
mov stage+91,stage+92 'DO NOT MODIFY.
add stage+93,h+3 'DO NOT MODIFY.
mov stage+92,stage+93 'DO NOT MODIFY.
add stage+94,h+2 'DO NOT MODIFY.
mov stage+93,stage+94 'DO NOT MODIFY.
sub stage+95,h+1 'DO NOT MODIFY.
mov stage+94,stage+95 'DO NOT MODIFY.
mov stage+95,h+0 'DO NOT MODIFY.
'Add code here to further process y if the call to put_y was deleted above.
jmp #main_lp 'DO NOT MODIFY.
'This subroutine acquires the next input sample (x) from the hub.
'It can be changed to acquire the sample in another way.
get_x rdlong x,par wz 'Read busy flag. Is it zero?
if_z jmp #get_x ' Yes: Keep checking.
rdlong x,arg_addr ' No: Read the input.
get_x_ret ret
'This subroutine writes the output of the filter (y) to the hub.
'It can be changed to deal with the output in another way.
put_y wrlong y,arg_addr 'Write result to hub.
wrlong zero,par 'Clear busy flag.
put_y_ret ret
'Constants and variables.
stage long 0[96] 'DO NOT MODIFY.
zero long 0
arg_addr res 1 'Hub address of argument.
x res 1 'DO NOT MODIFY.
y res 1 'DO NOT MODIFY.
h res 41 'DO NOT MODIFY.
Here, we see that the filter loop uses 312 instructions, exclusive of sample load and result store operations. With an 80 MHz clock, that would amount to 15.6 µs to process each sample, giving us a ceiling of 64K samples per second -- well within the design specs of 8000 samples per second.
We can run this object using the attached test program. (Note: FIR2PASM does not check to see if the PASM program fits in its cog. Some PASM programs may be too large. If that's the case, try reducing the precision or relaxing the filter requirements.)
Next, we can select and copy all 501 lines of numerical output from the PST window:
and paste it into the included Excel spreadsheet (fir_response.xls):
This gives us a chance to compare the actual frequency response with the one displayed by TFilter.
Enjoy!
-Phil





Comments
Any chance to make it work with 64 bits? Say, 24 bit samples, 16 bit coefficients
That might be a stretch. Every instruction, in that case, becomes two instructions. I think there's probably a better chance doing that with an IIR filter, where the number of taps can be less for similar performance. The problem with IIR filters, though (seen through my limited experience), is that that kind of precision might be required just to get the same performance I'm seeing here with the FIR filters.
-Phil
I've made some improvements to the tool in the past few days. It's sometimes desirable to have two filters that use the same set of coefficients. This comes in handy when processing stereo pairs or producing analytic signals (see below) from a single input. You now have a choice in the type of object produced:
Dual: two parallel channels
Dual Reversed: two channels, with "time reversal" in the second channel.
The code that computes the h*x factors is shared between channels when there are two channels. The actual computation of h*x can also be shared when the responses for both channels get computed from the same input. This is the quickest way to compute an output with both time forward and time reversed filters.
Now about that "time reversal" stuff. I came across a paper by Clay S. Turner, "An Efficient Analytic Signal Generator", which describes an alternative to the Hilbert transform that I described in this thread. The FIR filter Hilbert transform approximation delays all spectral components of a signal (within a given passband) by 90°, compared with the same signal delayed by half the filter's coefficient array size. This property can be used to attenuate image signals coming from an I/Q mixer, for example. One problem this method has is that there are ripples in the passband that are not mirrored by the delay line, which produces "leakage" when the filtered I and delayed Q signals are combined. Turner's paper describes an approach which alleviates this problem by designing a FIR filter that delays a signal by 45°. What's neat about his approach is that another filter with the same coefficients applied in time-reversed order will produce an output that leads the input by 45° and exhibits the same passband ripple. By applying one filter to the I signal and the other to the Q signal, the same relative 90° phase shift can be accomplished but with identical passbands. This results in less leakage when the two signals are combined.
Based on Turner's paper, I've created another web tool that calculates the FIR filter coefficients for one of these filter pairs:
Here's what it looks like:
You can select the number of filter coefficients, along with the passband. After pressing Submit, you are taken to the FIR2PASM screen with the coefficients filled in. Here is a typical result that I got from one of those filters:
Attached is a Spin program that demonstrates the phase shift for a chosen frequency. The results can be pasted into the included Excel spreadsheet and plotted, as I've done above.
-Phil
All of the passives and connections shown are already present in the Propeller Backpack; and the sigma-delta circuitry is adequate to filter the DUTY doody out of the generated signal.
Using the online TFilter program cited above, I created a narrow passband FIR filter and converted it to a PASM object. The signal generation cog, superposes two sine waves: 900 Hz, which is outside the passband; and 1300 Hz, which is inside. This is captured in a second cog via a sigma-delta ADC and sent to the filter cog, one sample at a time, at a rate of 20,000 samples per second. The output from the filter is then DUTY modulated and filtered onboard with an RC filter. That signal can then be viewed on an oscilloscope, along with the original, tapped from pin 0 with a high-value resistor:
Since the scope has built-in FFT capability, I was able to plot the result to see if the planned 30 dB minimum out-of-band suppression goal was met, and it was:
I need to do an I/Q mixer experiment next. It's a little harder to set up, so it may take some time to get it ready. 'More later!
-Phil
C.W.
The demo uses four cogs, not so much as a processing requirement, but because it needs eight counters, and there are only two per cog. In fact, once started, the I/Q local oscillators, the mixers, and the sigma-delta ADC don't require any code at all to operate. In brief, here's how the program works:
2. A0 is connected internally to the sigma-delta ADC on pins A9 and A10, which is left to run autonomously and whose phsa output is never read. Its only purpose is to provide an output on A9 that can be mixed with the two local oscillators. (I could have dispensed with this altogether and just used the DUTY mode output on A0; but typically this will be an analog input, and I wanted to simulate that condition as closely as possible.)
3. The two local oscillators (LO), I and Q are programmed to output square waves at 25000 Hz. The phase of Q lags that of I by 90 degrees.
4. The output of the ADC and those of the local oscillators are fed to two mixers comprised of logic-mode counters, programmed to count up only when the XOR of the inputs is true. This has the effect of multiplying the two inputs, which produces an output that includes the sum and difference of the LO and the incoming signal. In this case the difference signals are 25000 Hz - 24250 Hz = 750 Hz and 25500 Hz - 25000 Hz = 500 Hz.
5. The object of this exercise, then, is to separate the 750 Hz and 500 Hz mixer products without resorting to bandpass filters. This is important, because the two mixer products could have been much closer together in frequency than that. For example, they could represent two mutually interfering CW (Morse code) signals on either side of a receiver's beat frequency oscillator (BFO), or two single sideband (SSB) signals very close in frequency but on opposite sides of the BFO.
6. By using mixer products from both the I and Q mixers, we retain information about the phases of the two signals and not just their amplitudes. By applying ±45° phase shifts to the mixer outputs, we end up with two signals that can be added to isolate the signal from one side of the LO and subtracted to isolate the signal from the other.
7. These two mixer isolates can then be displayed on an oscilloscope and analyzed with the scope's FFT.
Here is what the two mixer products look like before filtering. The FFT of the bottom (cyan) trace shows the two frequency components as having equal amplitudes:
Here is what the filtered and combined mixer products look like. The "interfering" signal is virtually absent from each one. In fact, when viewed on a logarithmic scale, each undesired signal is about 33dB down from the desired one:
This software is a critical piece in my plan to make a software-defined radio that uses the Propeller. Basically my goal is to produce a superhet that uses a Propeller-mediated local oscillator to produce a 10 MHz intermediate frequency (IF), followed by prefiltering of the 10 MHz IF signal, then followed by I and Q mixers like what was demoed here. The mixer outputs could be filtered in various ways to demodulate AM, CW, SSB, FSK, and PSK signals, all in software.
-Phil
2. In furtherance of the filter change requirements, a stop method was added.
3. The output code is now AutoDoc (Gold Standard) compatible and includes the MIT license boilerplate.
I wasn't sure at first what to do about the copyright, since I'm not personally authoring the code every time it gets generated. But since the program used to generate the code and general formatting are mine, it seemed appropriate that the generated code should dwell under the same umbrella. This is despite the fact that the submitted parameters may well be proprietary to the user. It's the same with music: a melody may be copyrighted by its composer, but a recording of the performance of that melody is copyrighted by the performer or recording company. In this case, the downloaded program corresponds to the performance, not to the score (parameter list) from which it was performed. I'm not a lawyer, though, so I could have it completely wrong. In any event, it's MIT licensed, so the user can do pretty much whatever he wants with it anyway.
-Phil
I do not have the time to look at the full details at this time (too many other prop projects) so I have bookmarked it for later.
I have known for a long time it is possible to use just the counters from cog(s) without code. So the code could be used for other things. Thus we have access to 16 counters in the prop
But this project isn't really a "project" per se, but more of a brick in a much larger wall. Hopefully, I won't run out of counters before I'm done!
-Phil
-Phil
-Phil
Thanks.
Yet another outstanding piece of code, with great documentation to boot. I'm using this with good success in a receiver application; basically I'm using a NXP SA605 receiver IC with a 455kHz IF and very sharp 10kHz Murata ceramic filters to get good selectivity. Rather than use the phase detector on the SA605, I'm bringing the limiting amplifier output directly to the prop. I then use a counter to digitize the 455kHz waveform, and a simple cog to generate my second LO (precisely 455kHz), bringing my input signal to baseband. The FIR filter is then used to reject all the hash from the A/D conversion, the second LO, etc. This is working very well.
Question: In this role I'm occasionally getting what looks like symptoms of numerical overflow within the filter. These go away if I scale the input amplitude of the filter. Do you have a feel for maximum input amplitudes, or does this depend critically on the filter parameters? I.E. if we want to use 12-bit resolution, does that imply that if I keep the input magnitude less than 2^12 I should be OK?
Thanks!!
Mike
Wow! Man! That sounds like a very cool project, indeed; and I'm more than a little envious that you beat me to the punch! If you can spare further details, like a schematic and code, it would be very greatly appreciated.
Regarding the overflow: at this point, the only advice I can offer is empirical. Have you tried reducing the desired filter gain? There's an option for that in the online software. If you haven't tried it, please do, and let me know if it helps or not.
Thanks,
-Phil
Anyway, I was reading about the SoftRock SDR (software radio) and the use of the Tayloe Detector. Seems that this circuit is extremely simple. Now I guess that we cannot use the prop to generate the frequency outputs due to jitter in the counters? Is this correct? If not, then we could replace the Si570 with the prop and perhaps even generate the phase shift clocks meaning no 74xx74s either. Since we have multiple cores and pins, seems the prop may be able to also do the work done in the pc by the audio sampler too. Does this make sense and how much of this work have you done?
I also thought that the switching of the coils/caps could be done in a similar fashion to the way you switch sections in the backpack. i.e. by grounding a tap on a coil with a prop pin.
Unfortunately I have forgotten most of what I learnt in the early 70's about radios. Its a bit of old grey matter nowadays. However, the maths (when explained simply in summary form) is incredible in how to manage the signals in the digital realm. And it removes a lot of sources of noise too.
I've thought about the Tayloe Detector. My solution to the jitter problem is mix the signal to an IF frequency that's equal to the Prop's crystal frequency and do the "Tayloe" detecting with an I/Q detector in the counters. The LO for the mixer could then be set up as a VCO and frequency and phase locked to an internal Propeller clock via a DUTY-mode output.
Andrey Demenev presented another approach to the jitter issue, which I think is quite clever, by using the Propeller's Xin pin as the feedback in a PLL. The same propeller can then provide jitterless I and Q signals for direct conversion. A second Propeller chip is then used as a DSP to demodulate the mixer products.
BTW, I think you're right about the band-switching being possible by grounding coil taps or additional caps in the LC tank -- either directly by the Propeller, or indirectly via Prop-driven MOSFETs.
-Phil
At some point I'd like to play with a SoftRock. On a more immediate basis I'll probably be building a Tayloe detector for my personal use, as I want to build up a simple CW receiver with high sensitivity. Tayloe holds a patent on the basic detector and as far as I know has not licensed this to any vendor; I think from a legal/moral perspective one cannot sell a product infringing on his IP but I do think its within reason to build one for personal use.
Note: A lot of DDS chips (AD9834 comes to mind) have a built-in comparator which allows you to take the sine output, low pass filter it, and then generate a nice, clean, low phase noise square wave - perfect for driving something like a Tayloe detector. That's the approach I'd probably use rather than using the Prop's counters, as the phase noise from the prop's NCOs would likely preclude any serious work. Also, one thing I like about the AD9834 is that it has dual frequency and phase offset registers one can select with a pin - i.e. using this chip, once programmed by the Prop you can generate continuous phase FSK, or very sharp PSK using only single pins. Useful!
That brings up my RX topic; can't post the schematics immediately until I have time to draw something similar to my work for my employer on my own time. Reason: he owns the IP, not me. But here is the rough sketch of the idea for a simple FSK receiver:
RECEIVER: Use a SA605 receiver IC, with a loopstick antenna and split-C matching network (per data sheet) to receive HF signals. The IF frequency chosen is 455kHz, and I use two Murata CFULA455KB2A ceramic filters in the signal chain (very sharp!), with a resistive 6dB pad between the IF amp and the limiting amp. Assuming 4dB loss in my matching network, this gives an aggregate gain of about 98dB, with a total noise figure on the order of 30dB or so. Min detectable signal is around -105 to -107dBm. This is not spectacular, but definitely usable. One could improve this with a JFET pre-amp.
FIRST LOCAL OSCILLATOR: Drive the mixer section of the SA605 with an AD9834 direct digital synthesizer, using a 5th order analog reconstruction filter between the AD9834 output and the mixer input. This AD9834 is of course controlled by the Prop over a serial interface. As an alternative, you can use the oscillator section in the SA605, using the prop to adjust a varactor bias to tune the oscillator and a very high input impedance buffer to permit the Prop to discipline the oscillator. I didn't feel like doing a VCO (tricky, that), and wanted a simple means to generate low data rate minimum shift keying waveforms and the DDS fit the bill...
OUTPUT FROM SA605: The SA605 has a phase comparator for FM discrimination onboard. I didn't use that. Instead I bring the 455kHz IF output of the limiting amplifier to the prop. Specifically, I use a DC blocking capacitor (270-1000pF) and use a counter to build a sigma/delta ADC to digitize it. No decoupling caps are used as the PCB parasitics are large enough to perform that role. The feedback cap on the sigma/delta AGC is pretty large - 1 to 4.7 Meg. In addition I bring the RSSI output from the SA605 to the prop, using a resistive divider to scale the level to within the 3.3V maximum level for the Prop. This allows me to assess signal strength, and also recover on-off keying signals.
SECOND LOCAL OSCILLATOR: The second LO is formed in the Prop - specifically, I use a counter in NCO mode to generate a precise 455kHz square wave. A second counter is used in logic mode to effectively multiply this second LO with the received IF from the SA605 - thereby basebanding the input signal. The mixing operation is followed by a lowpass FIR filter running at 50ks/sec.
DETECTION: The signal may now be detected and decoding with some Prop code similar to what you did with the Bell 202 object, but with a mark/space offset more appropriate for the HF band.
ISSUE: Clock drift. If we have a tone offset of only 170Hz, it is reasonable to expect my clock reference for the first LO to drift a large fraction of the offset over a long period of time (despite using a TXCO reference for the DDS). Right now I "solve" that problem by using a pre-amble tone to my messages, and using the Prop to measure the frequency (and adjust the LO) by doing zero crossing counting - closing a poor man's AFC loop. One additional approach which comes to my mind is to exploit the phase comparator on the SA605, and tune my LO between my desired 2-FSK tones. Alternatively one could do the same thing in the Prop proper by implementing the phase comparison logic in software.
INPUT MATCH NOTE: The SA605's Gilbert Cell mixer has a very awkward input impedance (1500ohm) ; getting a lot of instantaneous bandwith froma split-cap matching network is difficult at best. Your best bet may be a varactor-tuned front end, driven by the Prop of course.
NOTES: The SA605 has a spectacular amount of gain in a small package. Therefore, it likes to break into oscillation given the slightest provocation. You will want to follow the SA605 evaluation board circuit layout as closely as you possibly can. Also - the SA605 severely punishes improper decoupling capacitor selection, or bad layout.
Mike
Seems to me that the SoftRock radio (the version that uses the Si570 as a programmable LO) concept could be ideal. What they do (as far as I can tell) is generate the quad phases from the Si570 LO using /4 counters/flipflops (74xx74 although surely this could be done with a single divider chain chip). These outputs control a quad mux (IIRC FST3253 but there are 74xx3253 available as well) that switches the RF input to 4 outputs which are summed in op amps to form the Tayloe detection. The output is centered around 22KHz (when the sound can do 44KHz resolution due to the Nyquist frequency). If the sound card can do ~96KHz then they centre around half of this being ~48KHz. So these outputs are fed to the PCs sound card and all the amazing maths is done in the PC.
What is interesting is that because the output center frequency is around 22KHz (first example) the image frequencies are now much easier to filter/reject by maths as it is only the audio that needs to be recovered.
So thinking about this, the PC side of the detection/filtering/maths may probably be quite easy within the prop chip and using the basics of what you are doing may in fact be quite (well relatively speaking WRT what you have already done) easy.
Since we still have prop resources available, the next part is how much of the other parts could also be put inside the prop? Bearing in mind that the softrock radio is now going up in freqencies to 144MHz (info for others reading this.. the 2m amateur band) and beyond. In fact some of the Si570 variants can go up to the GHz frequencies. As we've agreed, perhaps the band circuitry can also be switched with the prop. At the moment the softrock is plugging a little daughter board in for these bands. If we are going to want to go up into the 144MHz and beyond, then an external LO becomes more feasible as an extra because the Si570 is not cheap. This then solves the jitter problem anyway.
Your thoughts?
Ray
P.S. Don't you just love getting distracted with something so interesting! Makes my old 2m valve transcievers look pretty sick, and forgetting about the power drain! I had to carry a second 6V battery on the floor of my VW and I could only transmit for <2mins before I blew fuses
Ah, you want VHF. No problem! Some of the Silicon Labs parts are indeed pricey. However, its worth bearing in mind that you can always use the harmonic of a lower frequency DDS - suitably filtered and amplified it will do the trick at a more or less reasonable cost. There are also some reasonably high performance DDSes around that can easily generate VHF; see the AD9950 series... But these are at about the same price point as the Si Labs products.
I think the suggestion given to Phil about eliminating the jitter from the Prop NCO; still trying to get my head around it. If this is do-able one could just use a real VCO and prescaler, with the Prop mediating.
V/R
Mike
As for the Si570, yes they are expensive. I bet they are cheap in large qties though. But if we could reduce most of the ancilliary parts and control it with a prop, then all may not be lost. A really tiny CW/AM/SSB/FM receiver covering 1MHz-500MHz+ in a matchbox would be a real treat
Phil, seems what you have done is to simulate the section of the sdr (software defined radio) that encompasses the quadrature detector (74xx74 & FST3253) and amps (LT6231) plus the pc (including sound card) section. Is this correct? So what remains in the softrock radio is the bandpass filters and the oscillator (Si570)? If so, this is an absolutely brilliant piece of work!
The prop still has cores left to drive the Si570 and BPF selection. I would be quite happy to use an Si570 for the receiver if it could do 6m, 2m & 400MHz? bands too. For LF (180KHz-3MHz), an internal /4 inside the prop would be fine, and for HF (1.8MHz-30MHz) the Si570 may well not be required, depending on prop jitter.
First WOW. What a great thread and project.
I've been working with the Tfilter builder and your PASM code. I'm trying to work through it and understand how you're able to get such great performance. I'm trying to build a lowpass filter to run on 24-bit data before downsampling it. I've looked at a number of filters and I think I can get acceptable performance by using 8-bit coeffs. I choose this to avoid overflow during filtering. My question is how best to get those 8-bit coeffs. How does your PASM generating code convert type double coeffs (copied from Tfilter) into 8-bit? I assume when one selects the resolution on your webpage that it simply scales them. Would it be possible to spit out, in the PASM code our site generates, those values along with the original input (double) values? It would allow one to see the ideal coef and the actual coef.
And finally, do I understand that your perl code simply takes an (integer) coefficient and decomposes it into simpler math? For example c0 * 9 would be c0 << 3 + c0.
Thanks for this and all your contributions to the Prop community.
Peter
Thanks for the kind words!
Multiplication by a number in the open interval (-2, 2) can be achieved by shifting the number right to line up with each one bit in the multiplier and adding. The number of shifts and adds is equal to the number of one bits in the multiplier. This number can be reduced by converting the number to Canonic Signed Digit (CSD) form, as outlined in this paper:
In this representation, the initial binary multiplier is converted into two binary numbers: one whose one bits correspond to additions; the other, to subtractions. In this way the total number of one bits is minimized. In a FIR filter, all n coefficients, ci, are applied to the same input (X) at each time step. In that way, X can be shifted once for each one bit in the union of the 2n CSD coefficients. After each shift, whatever adds and subtractions required by the various ci can be performed before the next shift. Then the sum-of-product terms (the h's in the PASM program) can be shifted through the shift register to accumulate new products until being spit out the end as the FIR filter's output.
The actual CSD coefficients exist in the PASM code only as adds, subtracts, and shifts, not as numbers. In a future version of the Perl code, I could output these values as PASM comments. Another thing I plan to do at some point is to shift the X input left instead of right during the multiplies, then shifting the output right by the same total amount before outputting. This should lead to greater precision, since none of the X bits will get shifted out, losing carries into the LSB of the product. Not doing this may be the reason I was not able to obtain -60 dB suppression in my experiments. In doing so, it will be necessary to include the input range of X, so as to avoid overflows from the MSB. For a large range of X, a blend of left and right shifts may be necessary.
-Phil
Thanks for responding. While working on this project. I found the following whitepaper:
https://tagteamdbserver.mathworks.com/ttserverroot/Download/14883_firdesign.pdf
You may find it interesting, especially the part about interpolated FIR filters. Seems like some black magic there to me. You also may find section 10.2 interesting as it talks about the stop band attenuation as a function of bits. It may be that your suppression is bumping up against the filter limits (given the number of bits) and not accumulated error. Just a thought.
Regards,
Peter
-Phil
I've had more time to work with this and I've got a few plots to share. I'm very impressed with what you've done. To test this out, I used matlab to create a 50 second signal sampled at 10,000hz. This signal has sine waves at 5200hz, 2700hz, 2000hz, and 150 hz plus random noise. I saved these data as 24-bit integer values to an SD card and then read them into the prop and filtered them using a filter created on the TFilter website and PASM created on your site. I then saved those filtered data back to the SD card and read them back into Matlab for plotting against a few other filters.
Figure 1 below shows the original signal along with the filtered versions. Pretty hard to see what's going on but at least there aren't any gross errors. Figure 2 is the fft of the input signal (unfiltered). The spikes at 150, 2000, and 2700 correspond to the input sine waves. The peak at 4800hz is an aliased version of the 5200hz sine wave.
Figure 3 is the frequency response after filtering by a few different filters. The red filter was build using Matlab's Filter builder tool and was executed in Matlab using double precision. It has a higher passband corner and isn't exactly the same filter as what I made using TFilter. In many ways it's my "perfect" filter. The cyan curve is the one from the data filtered on the prop with 8-bit precision. The green and black are the filters from TFilter implemented in Matlab as floating point (green) and integer based (black). The agreement between the prop, webF, and webI is very strong. And it is clear that the 5200hz sine wave, aliases to 4800hz has been knocked down to nearly the background noise. This prop/PASM filter has 129 coefficients and performed all the necessary math on each input datum in ~80uSec by my measurement; plenty fast enough to keep up with real running at 10Khz.
I never calculated the time required to do this the prop in a more traditional fashion- standard multiply, but even using some of the clever Kenyen multiplying techniques, I'm sure this would not have been possible.
I've still got more work to do choosing the best filter to implement and benchmarking things, but the fact that it's even possible to do this much math at this speed is awe inspiring. In the end I'm building a decimation filter for different downsample rates of a 10Khz signal. I need to work on the interpolation and find the right filters for my different desired frequencies, but the work you've done here to make filtering possible is incredible. I'm still working through the concept and the PASM. I hope to understand it but for now it's a bit of magic and certainly magical.
Thanks,
Peter