Audio "Loudness" and Dynamic Range Compression
 Phil Pilgrim (PhiPi)
Posts: 23,514
Phil Pilgrim (PhiPi)
Posts: 23,514
I'm currently working on the driver object for Parallax's new Propeller-powered Scribbler II robot (S2). Those familiar with the original Scribbler (S1) will recognize that the audio volume was a bit on the wimpy side. There were a couple of reasons for this, which I won't go into here. Suffice it to say that, this time around, we're committed to providing a volume level that can be HEARD. One of the challenges is the tiny speaker, which will have to remain the same as that provided with the S1. Driving this speaker with a maximum amplitude square wave does provide a very loud response.
The Propeller, however, is capable of so much more than mere square waves, and the S2's audio section is designed to accommodate complex waveforms, such as speech and syntesized music. But these types of audio can encompass a wide dynamic range from soft to loud. And it's necessary to limit the amplitude of the soft parts, just so the loud parts don't overflow. The consequence for the S2 is that all but the loudest parts are back down in the mud. So what to do?
The solution I'm using is called "dynamic range compression". In the extreme, this would involve amplifying the bejeebers out of any signal and clipping it so that everything looks like a maximal-amplitude square wave. Obviously, such an approach would suffer extreme distortion and fidelity problems, so I've decided to take a softer approach. By modifying the instantaneous audio amplitude in software, using a non-linear transfer function, it's possible to make loud stuff loud and soft stuff louder. Due to the non-linearity, this does introduce some harmonic distortion. And therein lies the inevitable compromise: an increase in loudness at the expense of some fidelity. But in a robot environment with running motors and whining gearboxes, loudness holds most the trump cards, so the compromise is a reasonable one.
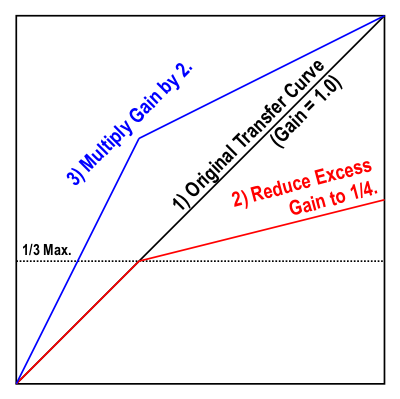
For simplicity in programming, I'm using a multi-step loudness boost function. At each step, the amplitude's absolute value is compared with 1/3 of its maximum allowed value. If it's less than that, no adjustments are made. If it's more than that, the amount of amplitude in excess of 1/3 max is divided by four. Next, in either case, the total amplitude is multiplied by two, and the sign (positive or negative) is restored. Here's a graph that shows the results of these steps:

The net outcome is that the peak amplitudes never overflow; but the average amplitude increases, resulting in greater perceived loudness. This process can be repeated any number of times. After each iteration the amplitudes of the soft parts are doubled, while those of the loud parts receive less of a boost. After an infinite number of such iterations, you end up with a step function: anything above zero goes to +max, and anything below zero goes to -max. This is the extreme case mentioned above.
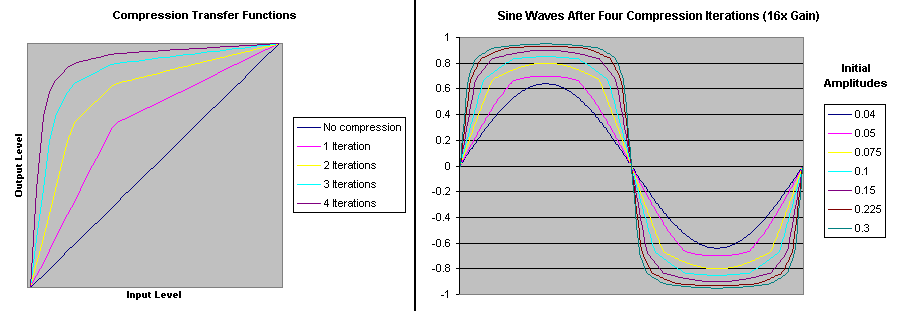
Here is a pair of graphs that show transfer functions for several iterations and the effects of a four-iteration compression on sine waves of various initial amplitudes:

Allpying this to the S2, I've found that Chip's vocal tract object works well up to a three-level (x8) compression, and that Johannes Ahlebrand's SIDcog can tolerate two levels (x4). In both cases, the volume level from the S2's speaker is more than adequate.
Here's the code I used to implement the compression in Chip's vocal tract object:
-Phil
_
The Propeller, however, is capable of so much more than mere square waves, and the S2's audio section is designed to accommodate complex waveforms, such as speech and syntesized music. But these types of audio can encompass a wide dynamic range from soft to loud. And it's necessary to limit the amplitude of the soft parts, just so the loud parts don't overflow. The consequence for the S2 is that all but the loudest parts are back down in the mud. So what to do?
The solution I'm using is called "dynamic range compression". In the extreme, this would involve amplifying the bejeebers out of any signal and clipping it so that everything looks like a maximal-amplitude square wave. Obviously, such an approach would suffer extreme distortion and fidelity problems, so I've decided to take a softer approach. By modifying the instantaneous audio amplitude in software, using a non-linear transfer function, it's possible to make loud stuff loud and soft stuff louder. Due to the non-linearity, this does introduce some harmonic distortion. And therein lies the inevitable compromise: an increase in loudness at the expense of some fidelity. But in a robot environment with running motors and whining gearboxes, loudness holds most the trump cards, so the compromise is a reasonable one.
For simplicity in programming, I'm using a multi-step loudness boost function. At each step, the amplitude's absolute value is compared with 1/3 of its maximum allowed value. If it's less than that, no adjustments are made. If it's more than that, the amount of amplitude in excess of 1/3 max is divided by four. Next, in either case, the total amplitude is multiplied by two, and the sign (positive or negative) is restored. Here's a graph that shows the results of these steps:
The net outcome is that the peak amplitudes never overflow; but the average amplitude increases, resulting in greater perceived loudness. This process can be repeated any number of times. After each iteration the amplitudes of the soft parts are doubled, while those of the loud parts receive less of a boost. After an infinite number of such iterations, you end up with a step function: anything above zero goes to +max, and anything below zero goes to -max. This is the extreme case mentioned above.
Here is a pair of graphs that show transfer functions for several iterations and the effects of a four-iteration compression on sine waves of various initial amplitudes:
Allpying this to the S2, I've found that Chip's vocal tract object works well up to a three-level (x8) compression, and that Johannes Ahlebrand's SIDcog can tolerate two levels (x4). In both cases, the volume level from the S2's speaker is more than adequate.
Here's the code I used to implement the compression in Chip's vocal tract object:
:boost [b]abs[/b] t1,x 'Boost: get |amplitude|.
:boost_lp [b]cmpsub[/b] t1,_0x2aaa_aaaa [b]wc[/b] 'More than 1/3 maximum value?
[b]if_c[/b] [b]shr[/b] t1,#2 ' Yes: Divide difference by 4.
[b]if_c[/b] [b]add[/b] t1,_0x2aaa_aaaa ' Add back to 1/3 max.
[b]shl[/b] t1,#1 'Multiply amplitude by 2.
[b]djnz[/b] t2,#:boost_lp 'As many times as gain calls for.
[b]shl[/b] x,#1 [b]wc[/b] 'Test sign of original amplitude.
[b]negc[/b] x,t1 'Replace with boosted value, signed.
-Phil
_


Comments
For example post-processing DDS output to flatten-out variations in amplitude across the frequency spectrum ...
Regards,
T o n y