Trying to find a mathematical relationship...
 Beau Schwabe
Posts: 6,575
Beau Schwabe
Posts: 6,575
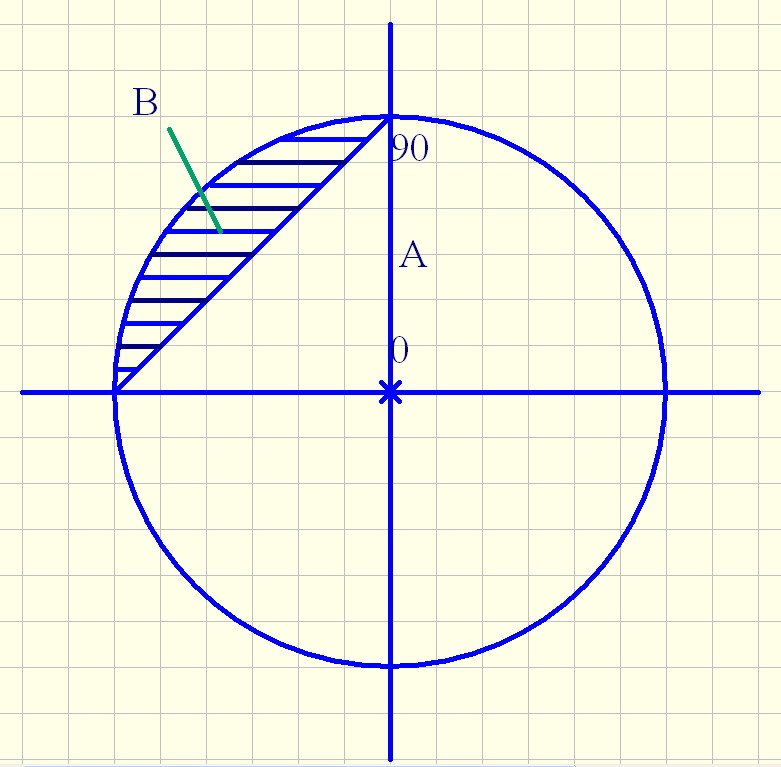
For a Propeller application, as 'A' goes from 0 to 90, I'm looking for the segment length of 'B' (See CORD attachment)... it would be easy if the segment length was not parallel to the horizon. The 'plot' looks like an air plane wing (See Graph attachment), but I don't think that is exactly what I'm looking for.
The table here shows the relationship...
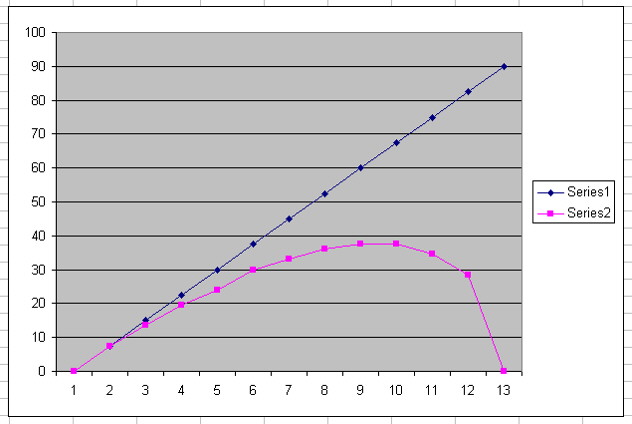
...and if you graph the two columns out you can see the 'air plane' wing. I'd rather not use a lookup table ... If anyone knows a formula I'd appreciate it.
Thanks
▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔
Beau Schwabe
IC Layout Engineer
Parallax, Inc.
The table here shows the relationship...
Deg Segment Length 0 0 7.5 7.5 15 13.5 22.5 19.5 30 24 37.5 30 45 33 52.5 36 60 37.5 67.5 37.5 75 34.5 82.5 28.5 90 0
...and if you graph the two columns out you can see the 'air plane' wing. I'd rather not use a lookup table ... If anyone knows a formula I'd appreciate it.
Thanks
▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔
Beau Schwabe
IC Layout Engineer
Parallax, Inc.


Comments
x^2 + y^2 = r^2
Eqn of Line
y = x + r
You know y (a), so we need to solve these equations for x
Circle x = sqrt( r^2 - y^2) (answer is positive or negative number)
Line x = y - r
Then you want the difference between the two numbers, the line is always less negative, so to get a positive answer
LineX - CircleX = B
y-r - (-sqrt(r^2 - y^2)) = B
or
y-r + sqrt (r^2 - y^2) = B
Or plugging in
A-90 + sqrt(90^2 - A^2) = B
Or, the same thing as mpark.
The Cartesian coordinates of a circle can be calculated from the formula X^2 + Y^2 = R^2 where R is the radius of the circle.
X on the circle (Xr) would be SQRT(R^2 – Y^2)
X on the chord (Xc) would be R – Y
B = Xr – Xc or (SQRT(R^2 – Y^2)) – (R –Y)
Y could be fixed steps between 0 and R or the sin of the angle between 0 and 90 degrees as required.
Wow, I think you nailed it right off the bat (See Series #3 in the attached image)... for some reason I just didn't see it. Thank you!
This is for a new (updated) accelerometer Demo using tilt as well as rotational deg, and I needed to know this length (or close approximation) mostly for the visual. I will post code soon to the OBEX.
▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔
Beau Schwabe
IC Layout Engineer
Parallax, Inc.
Video Demonstration
Source code available from the OBEX ... obex.parallax.com/objects/140/
In the video, the xTilt affects the horizontal level (blue)
The yTilt affects the horizontal up and down (white)
The Theta affects the inner 'ticks' (yellow) which is the rotational deg relationship between X and Y
▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔▔
Beau Schwabe
IC Layout Engineer
Parallax, Inc.
Post Edited (Beau Schwabe (Parallax)) : 12/22/2009 3:27:42 AM GMT