Integer calcs instead of floating point
In an earlier thread, @Mickster repeated a comment I've seen before but have never actually seen effectively presented. The comment is (paraphrasing) "if you need to use floating-point, you don't understand the problem".
My problem is this: I have a GPS that outputs its position in degs.decimal notation like this: -179.99999999. Assume for the moment that the GPS really can resolve its position to within 1/20th of an inch and that I actually need that degree of precision. (Go with it). I want to do some averaging of position over time, and then run some spherical trig calcs to plot GC position, crosstrack error, etc.
How do I even approach this problem using integers? The natural unit for trig is rads. My default approach would be to use double-precision IEEE math here, but this seems to be an unpopular approach. ![]()
The way I understand this, to reduce a simple GPS position in 3.8 format to a pure integer @ 32 bits means I'd have to down-scale the result by a pretty large factor (more than 8x) resulting in a precision loss. If I start doing math calcs, I'll further lose precision.
How does integer-only math get me where I need to be? Language is FlexBasic and the board is a P2 Rev C Eval.
ADDIT: actual gps output showing 3.8 format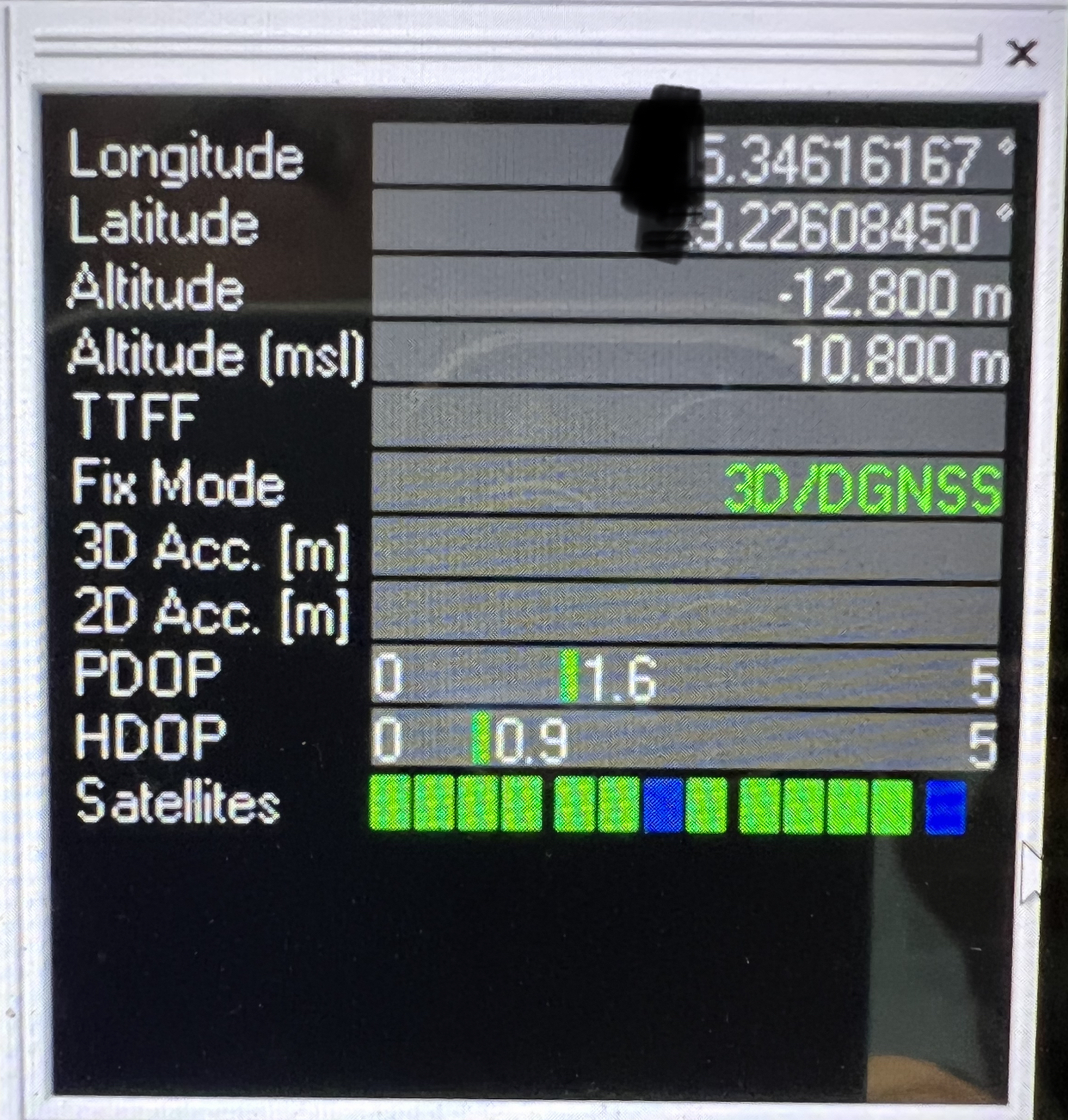


Comments
"need" is the operative word.
You can look at it from the opposite perspective too. If floats are already there and fast enough then they're just easier to use. If floats are not readily available or too slow then sure, integers can very much still work. But integers beyond simple arithmetic always needs more mental gymnastics ... multiplies blow out the top, and divides wash out the bottom. Maintaining dynamic range becomes a constant juggle of bit shifting.
BTW: Flex is limited to single precision floats. Good for maybe 7 decimal digits, eg: 3.4 format.
@evanh Exactly. And this limitation is the reason I'm interested in a possible integer-only approach.
32-bit ain't enough then either. Probably best to use string of digits approach. Same as pocket calculators use. It probably has a name but it's 6 AM and I'm off to bed now so not looking it up.
Mathematicians would like to claim so, but for computer math, integers/binrads are the correct way to represent absolute angles. Consistent precision over the entire range and automatic rollover.
To make use of the entire precision, you'd need to use 64 bit integers and presumably custom trig routines (P2 hardware only performs 32bit trig)
You could represent latitude and longitude as 0.32 fixed point numbers representing fractions of a circle. That would give you the most precision (about 9 decimal digits). Or you could try representing them as 64 bit fixed point numbers, with the point wherever you want. Either way you'd have to write your own trig routines; the 0.32 ones would be trival (that's the format used by the P2 CORDIC), 64 bit would be decidedly less so.
The 64 bit (longint) support in BASIC is somewhat usable now, with caveats (the main one being don't expect 64 bit literals to do what you want -- for now you'll have to build your 64 bit values by shifting and adding/oring smaller numbers).
@JRoark
RP2040 as a Co-Pro? Picomite (interpreted BASIC) does double precision and runs quite happily, overclocked to 378MHz
Craig
Hi,
As usual I am quite late in this discussion... Still it might make sense to use a local system of coordinates with a local zero point. So you only have to deal with differences to that zero and then 32 bits or single floats can be well sufficient.
Christof
+1
Another way to do this is to use two floats to hold the number -- one for the upper bits of precision, one for the lower. So you have two floats, x and y, and the true value of the result is actually x + y. You'll then have to manually construct functions to do addition, multiplication, and so on. This idea is usually called "double double" arithmetic, since traditionally it's used to increase precision of doubles, but naturally it will work for single precision as well:
https://en.m.wikipedia.org/wiki/Quadruple-precision_floating-point_format#Double-double_arithmetic
https://www.codeproject.com/Articles/884606/The-double-double-type
https://github.com/sukop/doubledouble
I have done a lot of Propeller programming over the years (mostly frequency measurement test equipment) and I have never used floating-point.
It comes down to knowing your data. Knowing the smallest and largest possible values for your data.
Choosing the correct "units" for your data, and being clever with how calculations are performed.
Sometimes I have to use two 32-bit variables (high,low) for some data operations. But that is still much faster than floating-point operations.
A common situation is having measure ticks (80MHz clocks) for longer than 26 seconds (could be 24 hours) with 1 tick resolution. If you lose 1 tick your measurement will be off.
We typically measure frequencies to uHz resolution in short gate times.
I think as a general variable type in a language floating-point is great. You don't have to worry about the data range (for the most part).
Bean
Here's something you might try. The idea is to put the integer part of the datum in one long (the high long as Bean suggests) and the fractional part in another. The trick is to convert the decimal fractional part into a binary fraction. IOW, you want 50000000 to convert to $8000_0000. So I wrote a program that that searches for a multiplier which, when multiplied by the decimal fraction, gives the correct binary fraction. It uses a binary search, along with a modified version of my umath object. The modification is to return any selected consecutive 32 bits from a 64-bit product of two unsigned 32-bit numbers. Here's the code:
CON _clkmode = xtal1 + pll16x _xinfreq = 5_000_000 INDX = 6 OBJ ser : "Parallax Serial Terminal" u : "umath" PUB start | i, incr, factor, z ser.start(9600) factor := $8000_0000 incr := $4000_0000 repeat i from 0 to 31 z := u.multindex(50000000, factor, INDX) ' ser.hex(z, 8) ' ser.char(13) if (u.lt(z, $8000_0000)) factor += incr elseif (u.gt(z, $8000_0000)) factor -= incr else quit incr >>= 1 ser.char(13) ser.str(string("factor == $")) ser.hex(factor, 8) ser.str(string(13, 13)) repeat i from 0 to 90000000 step 10000000 ser.dec(i) ser.str(string(" * factor = $")) ser.hex(u.multindex(i, factor, INDX), 8) ser.char(13) ser.dec(99999999) ser.str(string(" * factor = $")) ser.hex(u.multindex(99999999, factor, INDX), 8)Here's what the output looks like:
So, given an eight-digit decimal fraction, do this to it to get the binary fraction:
Once you combine the binary fraction with the integer part, you're left with a 64-bit fixed-point number that you can manipulate using normal extended integer math.
Attached below is an archive of the above program that includes the modified umath object.
-Phil
@Bean


It's great to see that you're still around, Terry
Craig
Sorry guys I'm have a lot of trouble here.
Tried to put some code in the previous post and it got mangled, so I tried to delete it, but I can't figure out how...
If you mean while editing....you can't (irritating). You just overwrite. I'm assuming that this is what you mean because I don't see anything actually posted.
Craig
https://forums.parallax.com/discussion/comment/1537968#Comment_1537968